Transformer

https://arxiv.org/abs/1706.03762

一、摘要

主流的序列转录模型主要依赖于复杂的循环或者卷积神经网络，其中包含编码器 (encoder) 和解码器 (decoder) 。在最好的模型中也会在编码器和解码器之间使用注意力机制。这篇文章提出一个新的简单的架构 —— Transformer ，这个模型仅仅依赖于注意力机制，而没有使用循环或者卷积。两个在机器翻译上的实验显示这个模型在机器性能上特别好，可以有更高的并行度和需要更少的时间训练。

二、结论

在这篇工作中，作者提出了 Tramsformer ，这是第一个完全基于注意力机制的序列转录模型，将广泛用于编码器-解码器架构的循环层替换为了 multi-head self-attention 。

对于翻译任务， Transformer 可以比其他架构快很多，且在实际数据小效果好。

这种基于注意力的模型可以被用于除文本以外的数据上，比如图片、语音、视频，使得生成 (generation) 不那么序列化也是研究的目标之一。

【如果机器学习代码开源，最好放在摘要的最后一句话】

三、导言

当时 2017 年最主流的时序模型是 RNN ，如 LSTM (long short-tern memory) 和 GRU (gated recurrent neural networks) 。其中有两个最主流的模型：语言模型 (language model) 和编码器-解码器架构 (encoder-decoder architectures) （输出的结构花比较多时）。

RNN 的计算特点是沿序列不断处理，对 $t$ 个输入，会根据前一个隐藏状态 $h_{t-1}$ 和第 $t$ 个输入计算当前隐藏状态 $h_t$ 。但这种处理模型有两个问题：第 $t$ 个输入必须等待前 $t-1$ 个输入都计算完成后才能开始计算，这导致计算无法并行；同时由于计算是逐步完成的，可能会导致时序早期的记忆信息在后期丢失。

在这之前 attention 已经被成功用在编码器和解码器中，主要用在如何将编码器的信息有效地传递给解码器。

四、相关工作

一些工作关注如何使用卷积神经网络替换循环循环神经网络来减少时序的计算。一个问题是用卷积神经网络对一些比较长的序列难以建模，因为卷积每次看的是一个非常小的窗口，只能通过叠加层数的方法使它们交互。如果使用 Transformer 模型里的注意力机制，一层就能够看到所有的序列。但卷积的一个好处是可以做多个输出通道，可以识别不一样的模式，为了达到这个效果，作者提出了多头注意力机制 (multi-head attention) 。

自注意力机制其实在之前的一些工作都有提到。

End-to-end memory network 不是用序列比对递归而是基于循环注意力机制，在简单语言问答和语言模型上表现良好。

Transfomer 是第一个只使用注意力机制来做编码器和解码器的模型。

五、模型架构

在众多序列模型中比较好的是编码器和解码器的架构，编码器将输入 $(x_1, \dots , x_n)$ 表示成 $\mathbf z = (z_1, \dots, z_n)$ ，其中 $z_t$ 是 $x_t$ 的向量表示。解码器拿到编码器的输出 $\mathbf z$ 生成一个长为 $m$ 的序列 $(y_1, \dots, y_m)$ ，其中 $n$ 和 $m$ 可以不等，和编码器不同，解码过程是一个个进行的。每一步都是自回归 (auto-regression) （过去时刻的输出也是当前时刻的输入）。

Transformer 遵循这种整体架构，对编码器和解码器使用堆叠的自注意和逐点、完全连接的层。

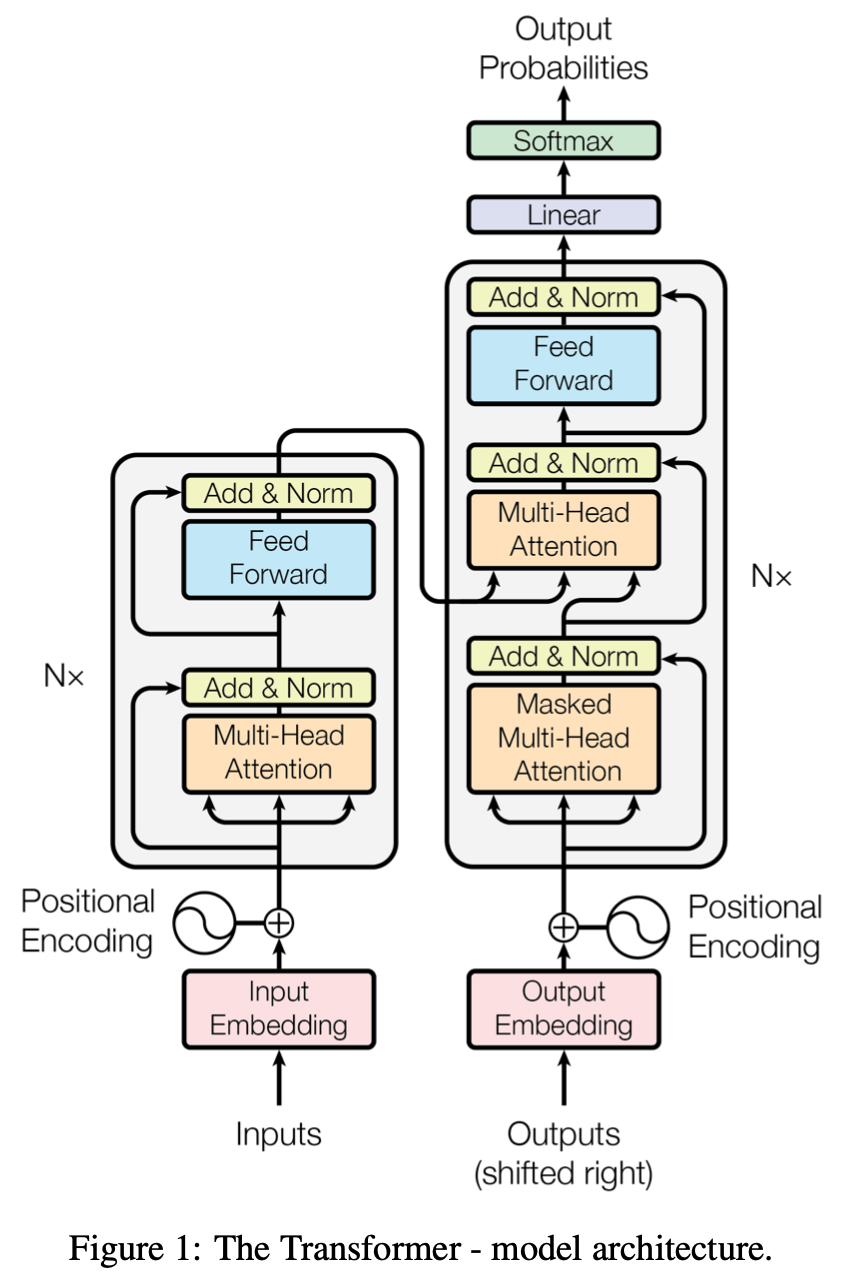
左侧是编码器，右侧是解码器。左侧灰框就是一个 transformer block ，里面只使用了一些注意力层、残差块和前馈神经网络。然后编码器的输出会作为解码器的输入，但在此之前会有一个掩码多头注意力机制。最后输出进入输出层，进行 softmax 。

1. 编码器和解码器堆栈

编码器：采用 6 个一样的层，每层有两个子层：multi-head self-attention mechanism 和 MLP 。对每个子层采用一个残差连接，最后使用层正则化 (layer normalization) ，即子层的输出是 $\text{LayerNorm}(x+\text{Sublayer}(x))$ 。由于残差块要求输入和输出大小一致，为了简化问题，规定所有输出的大小 $d_{model}$ 为 512 。

LayerNorm vs BatchNorm。考虑二维输入，每一行是一个样本 (batch) ，每一列是一个特征 (feature) 。 BatchNorm 是每一个 batch 中将一列（即一种特征）的均值变成 0 ，方差变成 1 。在预测时使用的是全部数据的均值和方差。 BatchNorm 有两个参数 $\lambda$ 和 $\beta$ ，可以将均值和方差缩放到指定值。 LayerNorm 则对每行（即每个样本）做正则化（均值为 0 ，方差为 1 ）。而 RNN 输入的是 3D 数据（每个样本是一个句子，每个句子有很多词，每个词是一个向量）。此时，行还是 batch ，列是序列长度 $n$ ，深度是 feature $d$ 。两者依然是切法不一样， BN 是按照 feature 切， LN 是按照 batch 切。在实际使用中， LN 使用的更多一点，因为在序列模型中，每个样本的长度可能会发生变化， BN 的结果的抖动幅度会比较大。而 LN 是每个样本自己算均值和方差，也不需要存储全局的均值和方差，更加稳定。

在变长的应用中一般不使用 BatchNorm 。

解码器：采用 6 个相同的层，每个层含有前面提到的两个子层和一个针对编码器输出的 multi-head attention 子层。同样使用了残差连接和 LN 。对解码器做的是自回归，即当前输出的输入集是前面时刻的输出，它在做预测的时候是不能看到之后那些时刻的输出。但在注意力机制中，每次能够看到完整的输入，所以在解码器训练的时候，为了避免在预测第 $t$ 个时刻的输出的时候看到 $t$ 时刻以后的那些输入，作者通过一个带掩码的注意力机制，保证训练和预测的时候行为是一致的。

2. 注意力层

注意力函数是一个将 query 和一些 key-value 对映射成输出的一个函数，其中 query 、 keys 、 values 都是向量。输出是 value 的一个加权和，所以输出的维度和 value 的维度是一致的。对于每一个 value 的权重，是根据 key 和对应 value 的相似度 (compatibility function) 计算得到的。其中注意力函数有很多方法。

接下来介绍 Transformer 用到的注意力。

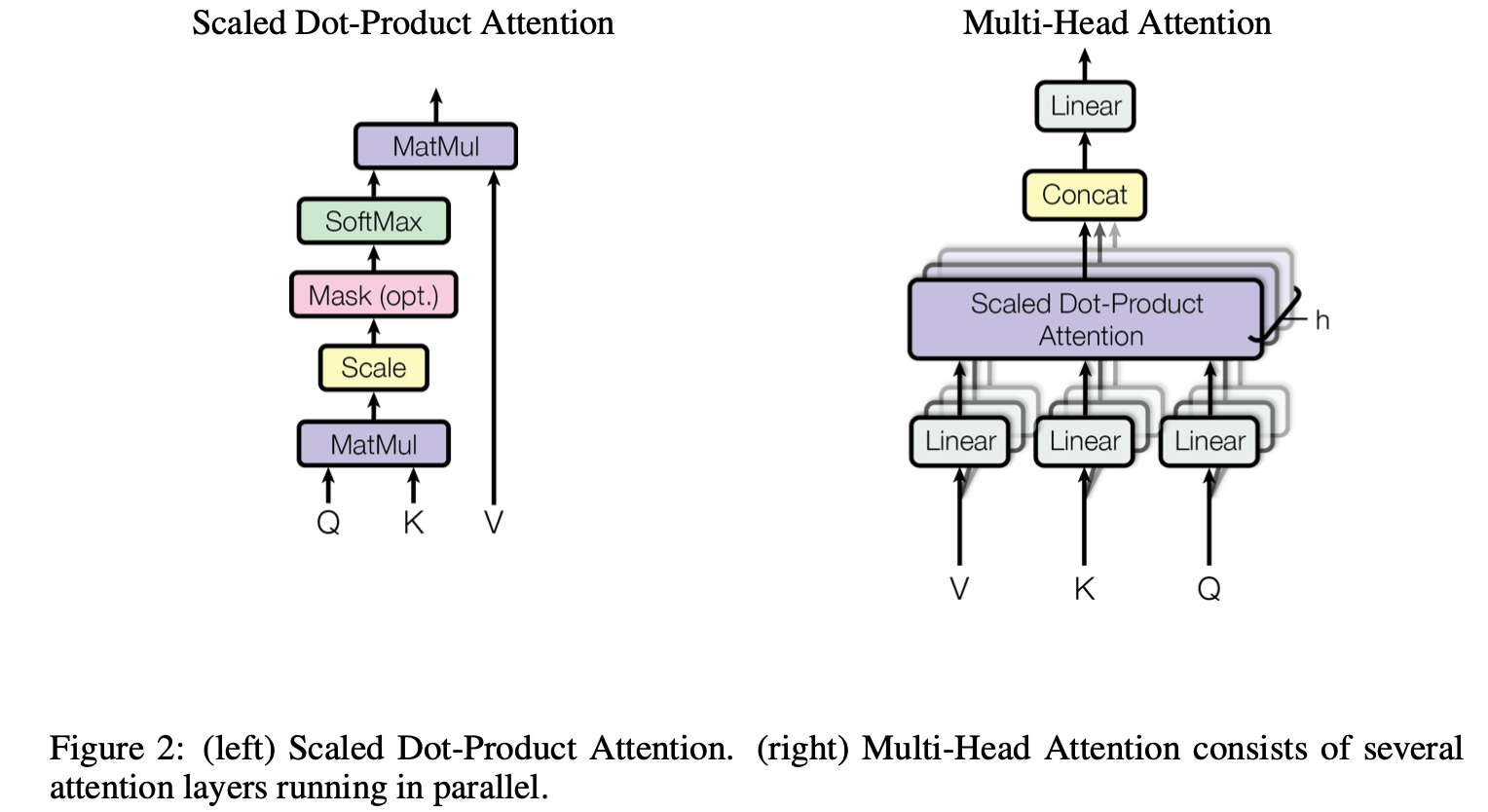
2.1 Scaled Dot-Product Attention

输入的 queries 和 keys 是等长的 $d_k$ ， values 的维度是 $d_v$ 。对每一个 query 和 key 进行内积，再除以 $\sqrt{d_k}$ ，再用 softmax 得到权重。这样所有的权重的和为 $1$ 。然后将这些权重作用在 values 上得到输出。

实际计算过程中需要并行计算，将不同的 query 写成一个 $n \times d_k$ 的矩阵 $Q$ ， keys 写成一个 $m \times d_k$ 的矩阵 $K$ ， values 写成一个 $m \times d_v$ 的矩阵 $V$ ： \(\text{Attention}(Q, K, V) = \text{softmax}(\cfrac{QK^T}{\sqrt{d_k}})V\) 那么这个注意力机制和其他的有什么不同？一般有两种注意力机制：加性注意力机制 (additive attention) 和点积注意力机制 (dot-product attention) 。除以 $\sqrt{d_k}$ 的原因是当向量长度比较长时点积的结果会相对比较大，之间的相对差距也会变大，最大值会更加靠近于 $1$ ，值向两端靠拢。此时梯度比较小，不利于反向传播。

然后需要看如何 mask 。假设 query 和 key 等长，且在时间上对应。之前的计算步骤一样的，只是在计算输出之前不要用到未来的东西。具体做法是 $t$ 时刻将点积结果中 $t$ 及其之后的值改为一个负的非常大的数，如 $-1e^{10}$ ，这样 softmax 之后这些权重都会变成 $0$ 。

2.2 Multi-Head Attention

与其使用单一的注意力函数，不如将整个 query、 key 、 value 投影到低纬 $h$ 次，再做 h 次的注意力函数。连接 (concat) 每个函数的输出，再投影回来，得到最终的输出。这么做的原因是 dot-product attention 中几乎没有可以学习的参数，但是有时我们希望可以识别不同的模式。有点类似于卷积网络中的多输出通道。 \(\text{MultiHead}(Q,K,V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O\\ \text{where head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)\\\) 其中 $W_i^Q \in \mathbb R^{d_\text{model} \times d_k}$ ， $W_i^K \in \mathbb R^{d_\text{model} \times d_k}$ ， $W_i^V \in \mathbb R^{d_\text{model} \times d_v}$ ， $W^O \in \mathbb R^{hd_v \times d_\text{model}}$ 。

在实际过程中 $h=8$ 。由于残差连接的存在，规定投影的维度 $d_k = d_v = d_\text{model}/h = 64$ 。

2.3 注意力在模型中的应用

Transformer 将 multi-head attention 用于三种途径：

• 编码器注意力：假设句子长度为 $n$ ，编码器的输入是 $n \times d$ 的向量。输入复制分成了 3 个，表示同样的东西既作为 key ，也作为 value ，还作为 query 。所以也叫做自注意力机制。编码器输出的大小和输入相同。不考虑多头和投影时，输出实际上是输入的加权和。权重来自于自己和其他所有向量的相似度的 softmax ，它和自己的相似度肯定是最大的。如果考虑多头的话，我们会学习 h 个不同的距离空间，使得结果不太一样。
• 解码器注意力 1 ：和上面一样的自注意力，只是有了 mask 。
• 解码器注意力 2 ：不再是自注意力。 key 和 value 来自于编码器的输出， query 来自解码器下一个 attention 的输入。对编码器的输入，根据解码器第一个子层的输出选出来。即解码器根据不同的输入，去解码器的输出里面挑选最感兴趣的东西。

3. Position-wise Feed-Forward Attention

其实本质就是一个单隐藏层 MLP ，对每个词使用一个相同的 MLP 。 \(FFN(x) = max(0, xW_1+b_1)W_2+b_2\) $x$ 的维度是 $512$ ， $W_1$ 将维度扩大到 $2048$ ， $W_2$ 将维度投影回 $512$ 。如果使用 pytorch 实现，其实就是两个线性层放在一起，不需要改任何参数，因为 pytorch 对于 3D 输入默认在最后一个维度做计算。

之前提到的 attention 起到的作用其实是将序列中的信息汇聚 (Aggregation) 。由于此时的结果已经有整个序列的感兴趣信息，因此 MLP 也就可以分开做了。

RNN 其实和 Transformer 相同，都是使用一个 MLP 来做语义空间的转换，不一样的是如何传递序列的信息： RNN 将上一个时刻的输出并入下一个时刻的输入，但在 Transformer 中通过一个 attention 层拿到整个序列的全局信息，然后用 MLP 进行语义转换。关注点都在于如何有效地使用序列的信息。

4. Embeddings 和 Softmax

输入是一个个 token ，需要映射成向量。 Embedding 就是给定任何一个 token ，学习一个长为 $d$ 的向量表示。在编码器输入、解码器输入和 softmax 之前都有一个 embedding ，它们共享相同的参数来简化训练。在每个嵌入层将权重乘以 $\sqrt{d_{model}}$ 。因为在学习 embedding 时会希望减小向量的 L2 Norm ，这样维度增大会导致权重减小。但是之后由于需要加入 positional Encoding ，这个不会随着向量的长度而改变大小。

5. Positional Encoding

attention 是不包含时序信息的，输出是 value 的一个加权和，权重是 query 和 key 之间的距离，和序列信息无关。这导致顺序变化但值不会变化。在 Transformer 中将位置 $i$ 加到输入中。 \(PE(pos, 2i) = \sin(pos/10000^{2i/d_\text{model}})\\ PE(pos, 2i+1) = \cos(pos/10000^{2i/d_\text{model}})\\\) 大概的思路是一个数字用一定长度 $512$ 的向量来表示，值是用周期不一样的 $\sin$ 和 $\cos$ 计算得到的。对结果放大 $\sqrt{d_k}$ 倍。

六、为什么要自注意力

作者比较了四种不一样的层：自注意力 (self-attention) 、循环层 (recurrent) 、卷积层 (convolutional) 、受限的自注意力层 (self-attention (restricted)) 。首先比较了计算复杂度，越低越好、顺序的计算（下一步计算必须要等前面多少步计算完成），越少越好、信息从一个数据点走到另一个数据点要走多远，越短越好。首先看自注意力层， $n$ 是序列的长度， $d$ 是向量的长度。复杂度是 $O(n^2 \cdot d)$ ，矩阵乘法的并行度很高，为 $O(1)$ ，一个 query 会和所有的 key 做运算，输出也是所有 value 的加权和，所以传输的长度是 $O(1)$ 。然后看一下循环层，如果序列长度为 $n$ ，就一个个做运算，每个里面计算$n \times d$ 乘以 $d \times ？$ 的 $W$ 矩阵，根据矩阵的并行计算，最小的并行单元的计算复杂度是 $d^2$ ，所以总的计算复杂度是 $n \cdot d^2$ 。但是由于一步步做运算，当前时刻的计算需要等待前面时刻的结果，在并行性上只有 $O(n)$ ，而且最初点的历史信息需要走过 $n$ 步才能传递过去，所以传递的长度是 $O(1)$ ，所以 RNN 不善于处理特别长的序列。然后看下卷积层，在序列上采用的是 $1d$ 卷积，卷积核大小 $1 \times k$ ，输入输出的通道数为 $d$ ，所以计算复杂度是 $k \cdot n \cdot d^2$ 。但是卷积操作的并行度很高，为 $O(1)$ ，另外每个 token 一次只能看到一个 kernel 大小的窗口，在距离 $k$ 以内一次就可以完成信息传递，所以传输的长度是 $O(\log_k(n))$ 。最后看看受限的自注意力层。 query 只和最近的 $r$ 个邻居做运算，这样减少了计算复杂度 $n^2 \cdot d$ ，但也增加了传输的长度 $O(n/r)$ 。

实际上 attention 对整个模型的假设更少，导致需要更多的数据和更大的模型才能训练出和 RNN 、 CNN 相同的效果，因此现在基于 transformer 的模型非常大和贵。

七、实验

1. 训练数据集和 batching

WMT 2014 英语-德语数据集，其中含有 450 万个语句对，采用 bpe 编码，有共享的 37000 个 token 。共享的好处是不需要两个字典，编码器和解码器的 embedding 可以使用同一个。以及 WMT 2014 英语-法语数据集。

2. 硬件和 schedule

使用 8 个 P100 的 GPU 。小模型，一步 0.4 s，训练 100000 步，12 个小时。大模型，一步 1 s，训练 300000 步，3.5 天。

3. 优化器

学习率： \(lrate = d_\text{model}^{-0.5} \cdot \min(step\_num^{-0.5}, step\_num \cdot warmup\_steps^{-1.5})\)

4. 正则化

Residual Dropout：每一个子层，在输出上，进入残差连接和 LN 之前，使用 dropout ；在 embeddings 和 pe 求和之前也用了 dropout ， dropout 率是 0.1 。

Label Smoothing：将 0 和 1 适当靠里，这会增加模型的不可信度，但会增加精度和 BLUE 。

八、结果

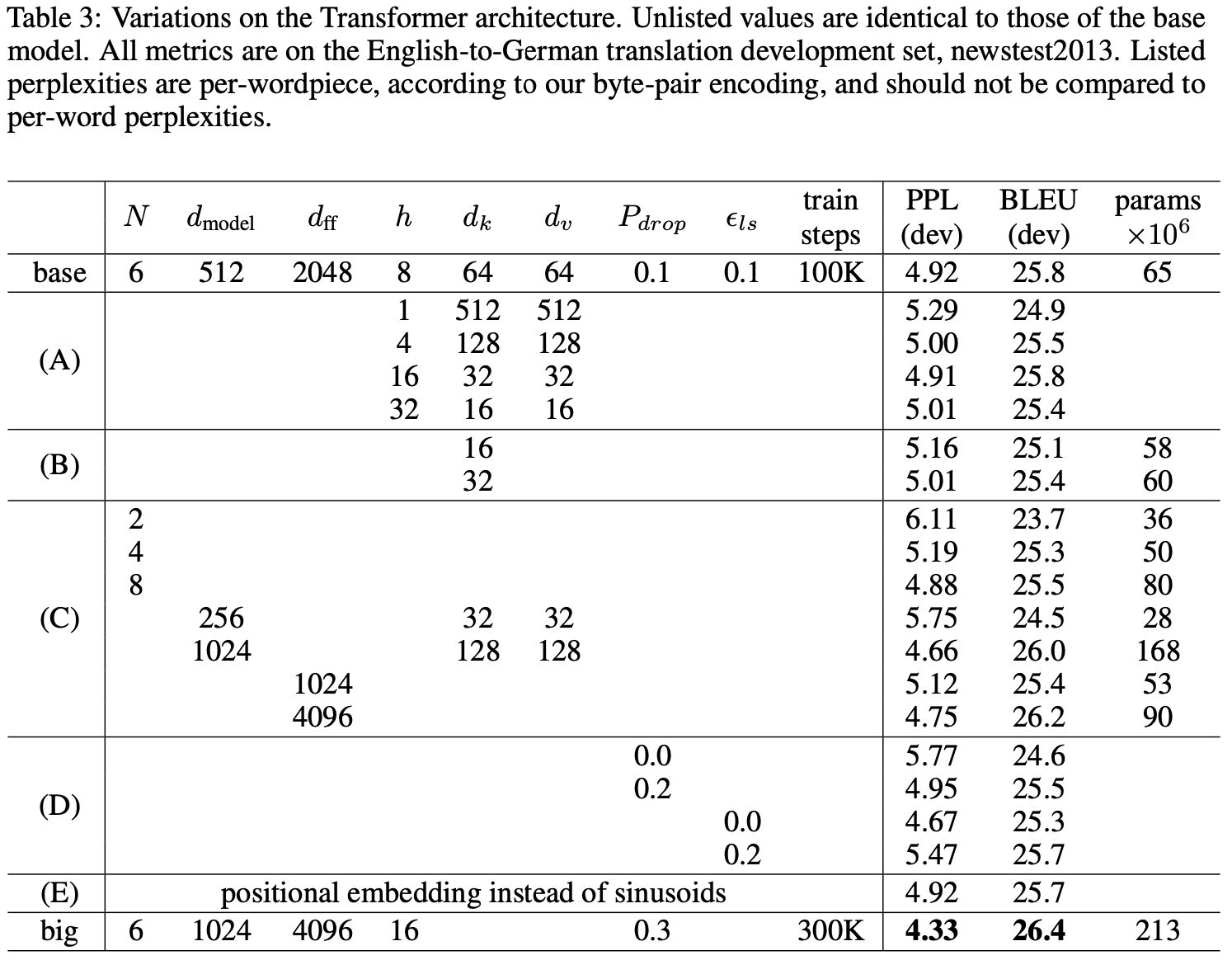
九、评论

这篇文章写作非常简洁，也没有用太多技巧。写作时最好适当减少不重要的内容，讲清楚故事，为什么要做这件事，以及设计的理念。

Transformer 已经在各种领域都有进展。

标题依然说只需要 attention ，但实际上 Transformer 中的残差块和 MLP 缺一不可。attention 不会对数据的顺序做建模，却能够超过 RNN ，现在研究认为它使用了一个更广泛的归纳偏置，使得它能处理一些更一般化的信息。这也就是为什么 attention 并没有做任何空间上的假设却能超过 CNN ，但是它的代价是因为假设更加一般，对数据抓取信息的能力变差，所以需要更多的数据、更大的模型才能训练出需要的效果。

如果觉得本教程不错或对您有用，请前往项目地址 https://raw.githubusercontent.com/Harry-hhj/Harry-hhj.github.io 点击 Star :) ，这将是对我的肯定和鼓励，谢谢！

作者：Harry-hhj，Github主页：传送门