RM 教程 6 —— 特征点,双目相机与光流
机械是肉体, 电控是大脑, 视觉是灵魂
特征点
给你两张从不同视角拍摄同一物体的图片,一个常见的任务便是找到该物体在两张图片中对应的像素位置。解决这一问题的方式通常是特征点。特征点通常是一些角点,边缘点,在这些地方通常有较高的像素梯度,使得我们可以十分轻松地通过局部算子的响应来找到这些点。角点检测的算法比较著名的是Harris算法,具体在本教程内不展开。同时,为了进行匹配,我们必须用定量的方式来描述这些角点,使得我们能够仅仅比较这些定量描述向量的距离,便可得知两个特征点之间的相似程度。
从而,我们便得到了特征点的两大重要概念,Keypoint关键点和Descriptor描述子。
ORB-FAST
这里将以ORB-FAST特征点举例,来讲解特征点检测算法。
FAST-N也是一种角点检测算法,它遍历每一个像素点,比较以点为中心半径为3的圆上的各个点像素值与中心点的像素值,若周围有连续N个点的像素值不落在中心点像素值的(设定好阈值的)邻域内,便称该点为一个角点,或者说特征点。我们通常使用FAST-12,这个算法有一个加速,即先检测1,5,9,13这四点,若这四点有三个及以上不落于邻域内,则才可能为一个角点。

当然以上算法可能形成大量角点,通常采用Harris响应值(详见Harris算法)来做非极大值抑制(NMS),即某一邻域内只保留响应最大的那个角点。
以上算法我们可以在多尺度下完成,并通过计算灰度质心来获得关键点的方向信息,这样获得的特征点便具有了尺度和方向不变性,相比原先的FAST特征点更加鲁棒。
此外,我们通过特征点的方向,对图像进行旋转,然后在点周围随机取128对点(p,q),我们的描述子便可表征为一个128维向量。各对点对应向量的各个维度,当p点的灰度值大于q时对应维度的值便为1,反之为0。故而,值得注意的一点便是我们比较ORB的描述子时采用Hamming距离(即异或运算)而非欧式距离。
下面便是实践环节,本教程的实践均基于唐欣阳学姐前部长在上个赛季布置的作业,即进行一个图像全景拼接的过程。
我们对以下的两张在不同视角用同一相机拍摄的对于同一场景图片的进行特征点生成与匹配


代码如下
读入图片并转化为灰度图
int main(int argc,char** argv)
{
namedWindow("show",WINDOW_NORMAL);
resizeWindow("show",800,600);
// read two images
Mat img1 = imread("../stereo-data/0_orig.jpg");
Mat img2 = imread("../stereo-data/1_orig.jpg");
// using gray image to compute
Mat gray1,gray2;
cvtColor(img1,gray1,COLOR_BGR2GRAY);
cvtColor(img2,gray2,COLOR_BGR2GRAY);
创建ORB特征点检测器,opencv提供其为一个智能指针对象,create函数具体参数较为复杂,如有兴趣可自行查看文档和阅读ORB相关资料以了解更多其原理。 当然在这之前n_features还是可以调调参的,默认为500个点。
//create orb detector
Ptr<ORB> orb = ORB::create();
检测关键点
// create the container of Key points
vector<KeyPoint> feature_points1,feature_points2;
// do Orient_FAST detect Keypoint
orb->detect(gray1,feature_points1);
orb->detect(gray2,feature_points2);
根据关键点计算描述子,描述子用Mat矩阵存储,你会发现这是一个$500\times 32$的矩阵,其中元素均为uchar类型即128bit,存储上述的128维特征向量,通过位运算大大提高了计算速度。
// compute the descriptors
Mat descriptor1,descriptor2;
orb->compute(gray1,feature_points1,descriptor1);
orb->compute(gray2,feature_points2,descriptor2);
进行暴力匹配,使用Hamming距离
//do matching
//create Matcher
BFMatcher matcher(NORM_HAMMING); //O(N^2)
vector<DMatch> pairs;
matcher.match(descriptor1,descriptor2,pairs);
printf("DMatch contains the matched points like (%d in img1,%d in img2) their distance is %.3f (in Hamming Norm).\n"
,pairs[0].queryIdx,pairs[0].trainIdx,pairs[0].distance);
显示匹配结果
//draw the matched pairs and show
Mat canvas;
drawMatches(img1,feature_points1,img2,feature_points2,pairs,canvas);
imshow("show",canvas);
waitKey(0);
通过筛选,选择距离较小的匹配点,作为较好(good)匹配,通常我们会使用较好匹配作后续处理
//You can also filter the match to generate
vector<DMatch> good;
double min_dist = 100000;
// compute the minimum of the distance
for(const DMatch&m:pairs)
{
if(m.distance < min_dist) min_dist = m.distance;
}
// filter
for(const DMatch&m:pairs)
{
if(m.distance < max(min_dist*2,30.))
{
good.push_back(m);
}
}
drawMatches(img1,feature_points1,img2,feature_points2,good,canvas);
imwrite("../good_match.jpg",canvas);
imshow("show",canvas);
waitKey(0);
较好匹配的效果如下

画出特征点,你可以看到特征点的方向以及描述子的大小
// draw the keypoint
drawKeypoints(img1,feature_points1,canvas,Scalar::all(-1),DrawMatchesFlags::DRAW_RICH_KEYPOINTS);
imwrite("../keypoints.jpg",canvas);
imshow("show",canvas);
waitKey(0);
return 0;
}

将上述代码封装为函数,供后续算法使用
除了ORB特征点,还有SIFT特征点等,他们的使用与ORB类似,就不展开了。
2D图像的匹配
在比赛中,我们的车辆是运动的,我们是否有办法知道相邻图像之间相机拍摄角度的位姿变化呢?这样的话,我们也能确定车辆的位置变化。、
上面全景匹配问题,我们如何将一张图片的像素点转换到另外一个视角下的样子,以完成匹配呢?
两张图片的匹配,是一个单目匹配问题。在这里,我们不知道两个视角之间的位姿关系。而在双目视觉中,我们知道两个视角之间的位姿关系,这将在后面描述。
下面介绍一些重要概念。
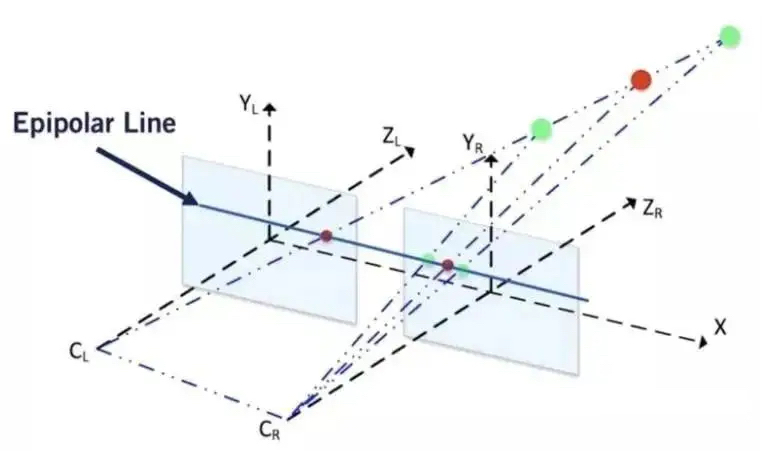
对极约束
对极约束是一个非常漂亮的公式,下面来一起推出它!
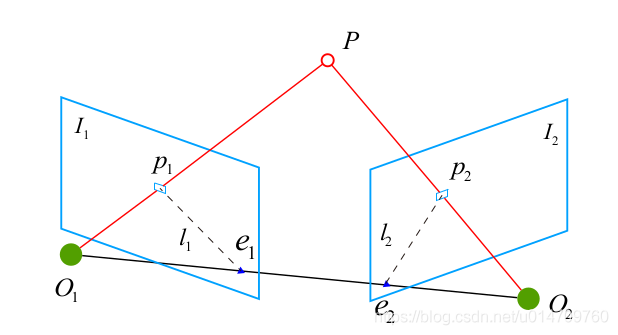
首先,如图所示,p1,p2是一对已经匹配好的对应点,即它们在空间中对应同一物体P
我们称向量$\vec{e_1p_1}$ $\vec{e_2p_2}$ 所在的直线为极线,$O_1PO_2$为极平面,$O_1O_2$为基线,这张我们后面还会用到
在上两节课中,我们知道了这些公式 \(z_1p_1 = z_1 \left[ \begin{matrix}u_1\\v_1\\1\end{matrix}\right] = KP_1\\ z_2p_2 = z_2 \left[ \begin{matrix}u_2\\v_2\\1\end{matrix}\right] = KP_2\\ P_2 = RP_1+t\) 其中$R,t$为视角1到视角2的位姿变化,未知。
设归一化相机坐标系下,有 \(x_1 = K^{-1}\left[ \begin{matrix}u_1\\v_1\\1\end{matrix}\right] \\ x_2 = K^{-1}\left[ \begin{matrix}u_2\\v_2\\1\end{matrix}\right]\)
下面的等式被称为up to scale等式,即两边在任意一边乘上一个非零常数后相等
如$2 = 1$就是一个up to scale等式
则有下面式子,等式两边差深度因子 \(P_1 = K^{-1}\left[ \begin{matrix}u_1\\v_1\\1\end{matrix}\right] = x_1\\ P_2 = RP_1+t = K^{-1}\left[ \begin{matrix}u_2\\v_2\\1\end{matrix}\right] = x_2\) 即 \(x_2 = Rx_1+t\\ t\times x_2 = t\times(Rx_1+t) = t\times Rx_1 + t\times t\) 显然 $t\times t = 0$
我们试着两边对$x_2$做内积,这是因为大学物理或者高等数学告诉我们,$t\times x_2$是垂直于$x_2$的 \(x_2^T(t\times x_2) = x_2^T(t\times Rx_1) \\ 0 = x_2^T(t\times Rx_1)\) 根据up to scale的定义,我们知道下面这个式子在正常等式下也成立 \(x_2^T(t\times Rx_1) = 0\) 这里补充一个概念 \(\left[ \begin{matrix}a_1\\a_2\\a_3\end{matrix}\right]\times \left[ \begin{matrix}b_1\\b_2\\b_3\end{matrix}\right] =\left| \begin{matrix}\vec{i}&\vec{j}&\vec{k}\\a_1&a_2&a_3\\b_1&b_2&b_3\end{matrix}\right|=\left[\begin{matrix}0&-a_3&a_2\\a_3&0&-a_1\\-a_2&a_1&0\end{matrix}\right]\left[\begin{matrix}b_1\\b_2\\b_3\end{matrix}\right] = a^{\ \hat{}}\ b\) 则 \(x_2^Tt^{\ \hat{}}Rx_1 = 0\) 该式便称为对极约束,当然像素值的对极约束为 \(p_2^T{K^{-1}}^Tt^{\ \hat{}}RK^{-1}p_1 = 0\) 可以改写为 \(x_2^TEx_1 = 0\\ p_2^TFp_1 = 0\) $E$称为essential matrix本质矩阵,来源其尺度不变性,即对$\forall\alpha\in \mathbb{R} , \alpha E$仍然为一个可行的本质矩阵,这在于平移向量$t$的尺度,在这里也表现出了单目的尺度不确定性
$F$称为fundamental matrix基础矩阵,可以从$E$导出,在于你有没有完成上上周的相机标定任务,由于$K$一般已知,且$E$形式更为简单,我们通常估计$E$
利用我们匹配的特征点对,可以列出多个对极约束方程 \({x_2^i}^TEx_1^i = 0\\ E = \left[\begin{matrix}e_1&e_2&e_3\\e_4&e_5&e_6\\e_7&e_8&e_9\end{matrix}\right] \rightarrow e = \left[\begin{matrix}e_1\\e_2\\e_3\\e_4\\e_5\\e_6\\e_7\\e_8\\e_9\end{matrix}\right]\)
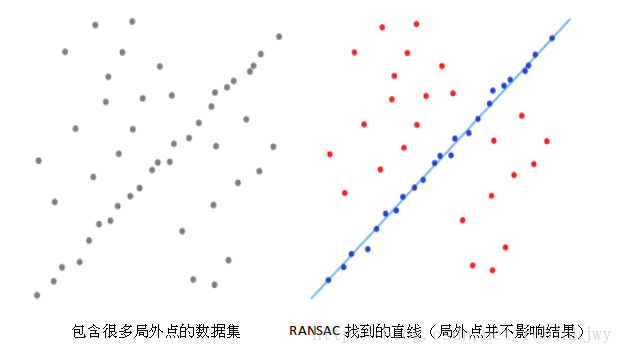
实际上可改写为一个线性方程组,我们用至少8组特征点构造一个$8\times 9$的$A$矩阵,实际求解会用RANSAC方式来优选匹配,排除误匹配 \(Ae = 0\)
RANSAC简介
RANSAC,随机采样一致性算法,是一种迭代算法,其本质思路是对数据集随机采样出数个子集,在这些子集上对原问题进行估计,并计算估计指标(比如MSE等),若指标低于设定阈值,则采纳该子集,将其元素作为inlier(内点),每次迭代,我们在随机采样的各个子集中选择最优子集,即内点最多的一个子集,以其评估的参数作为该次迭代的结果,然后根据迭代停止条件(如迭代最大次数,设定迭代停止阈值等)选择继续迭代还是停止返回结果。
解线性方程求解$E$,由于$E = t^{\ \hat{}}R$, 对$E$做SVD分解,便能求解$R$和$t$,同时$E$的特征值的约束使得我们能够求出$E$的形式。这里详细过程涉及矩阵论知识就不展开了,opencv已经帮我们封装好了。
这些都是一些数学,虽然美,但是也比较烦,我们还是来看看怎么实际操作。
读入相机内参
1
2
3
4
5
int main(int argc,char** argv)
{
// camera matrix
FileStorage params("../camera.yaml",FileStorage::READ);
Mat K = params["K"].mat();
找特征点,已经封装成函数,输入图片,输出较好匹配的对应点集
1
2
3
4
5
Mat img1 = imread("../stereo-data/0_orig.jpg");
Mat img2 = imread("../stereo-data/1_orig.jpg");
vector<Point2f> left_pts;
vector<Point2f> right_pts;
find_match(img1,img2,left_pts,right_pts);
解本质矩阵,使用RANSAC方法
1
2
3
// find the Essential Matrix using RANSAC
Mat E = findEssentialMat(left_pts,right_pts,K,RANSAC);
cout<<"Essential Matrix is \n"<<E<<endl;
最后分解E,得到R和t,这里输入对应点为了代入排除矩阵分解时的多解,值得注意的是,解得的平移向量t是归一化过的,我们并不知道它的单位,即其具有尺度不确定性,这也是单目估计的弱点所在。
1
2
3
4
5
6
7
Mat R,t;
recoverPose(E,left_pts,right_pts,K,R,t);
cout<<"R is \n"<<R<<endl;
cout<<"t (unknown unit) is \n"<<t<<endl;
return 0;
}
这里尺度不确定性可以通过补充深度信息来解决,从而实现通过反投影方式来进行图像拼接,不过在此之前,我们先来介绍一下另外一种进行直接二维映射的图像拼接方式。
实际上,此处估计出的相机运动信息通常不恢复其尺度至常见单位,而是基于初始化来固定尺度,通常做法有将初始化时所有特征点深度设为1(比如对着一面墙来初始化),或者就像这样将平移向量$t$归一化,但这样后续计算会不稳定。
单应矩阵
回顾此式,注意该式为up to scale \(P_1 = K^{-1}\left[ \begin{matrix}u_1\\v_1\\1\end{matrix}\right] = x_1\\ RP_1+t = K^{-1}\left[ \begin{matrix}u_2\\v_2\\1\end{matrix}\right] = x_2\) 假定所有的特征点落在同一平面上,则有 \(n^TP_1+d = 0\\ -\frac{n^TP_1}{d} = 1\) 则 \(p_2 = K(RP_1-\frac{n^TP_1}{d}t) = K(R-\frac{t}{d}n^T)P_1 = K(R-\frac{t}{d}n^T)K^{-1}p_1 = Hp_1\) 其中$p1,p2$均为像素点(可以在去畸变后再进行特征点匹配,本教程例子均不考虑畸变)
这样只需求出单应矩阵$H$便可,实际上$H$是一个透视变换矩阵,这你们在上节课学过
那么有 \(H = \left[ \begin{matrix}h_{11}&h_{12}&h_{13}\\ h_{21}&h_{22}&h_{23}\\ h_{31}&h_{32}&h_{33}\end{matrix}\right]\) 则有 \(\left[ \begin{matrix}u_2\\v_2\\1\end{matrix}\right]= \left[ \begin{matrix}h_{11}&h_{12}&h_{13}\\ h_{21}&h_{22}&h_{23}\\ h_{31}&h_{32}&h_{33}\end{matrix}\right]\left[ \begin{matrix}u_1\\v_1\\1\end{matrix}\right]\) 则有两对约束 \(u_2 = \frac{h_{11}u_1+h_{12}v_1+h_{13}}{h_{31}u_1+h_{32}v_1+h_{33}}\\ v_2 = \frac{h_{21}u_1+h_{22}v_1+h_{23}}{h_{31}u_1+h_{32}v_1+h_{33}}\) 通过这两对约束,基于四对匹配特征点,我们同样可以获得$8\times 9$矩阵$A$ \(A\left[ \begin{matrix}h_{11}\\h_{12}\\h_{13}\\ h_{21}\\h_{22}\\h_{23}\\ h_{31}\\h_{32}\\h_{33}\end{matrix}\right] = b\) 解得$H$,并且也可通过矩阵分解来获得$R$和$t$,详细过程略过
下面同样是实践环节,在本环节,我们将进行图像拼接,在这里我们假设所有点在同一平面,这样效果可能不好,但值得一试。(由于opencv没有提供api进行$H$的分解计算,想了解从$H$得到$R$和$t$可参考opencv_$version$/samples/cpp/tutorial_code/features2D/Homography/pose_from_homography.cpp例程)
求解$H$单应矩阵的函数,和上面求解$E$类似
void find_Trans_H(const Mat &img1,const Mat &img2,Mat& H)
{
vector<Point2f> lpt,rpt;
find_match(img1,img2,lpt,rpt);
H = findHomography(lpt,rpt,RANSAC);
}
进行图像拼接的函数。对于图像透视变换后其投影位置在原图像外,一个比较简单的解决方法是增大展示的画布大小,这样便需要对原图像进行一定平移使其展示在画布中心。若对原图像进行了平移,那么投影的图像其投影位置也要进行平移,可以用如下函数 \(u_2 + \delta u = \frac{(h_{11}+\delta u \cdot h_{31})u_1+(h_{12}+\delta u \cdot h_{32})v_1+(h_{13}+\delta u \cdot h_{33})}{h_{31}u_1+h_{32}v_1+h_{33}}\\ v_2+\delta v = \frac{(h_{21}+\delta v \cdot h_{31})u_1+(h_{22}+\delta v \cdot h_{32})v_1+(h_{23}+\delta v \cdot h_{33})}{h_{31}u_1+h_{32}v_1+h_{33}}\) 通过改动$H$,我们在基于warpPerspective函数进行变换的时候能对投影位置进行相应的平移。
void process_Stitch(const Mat& img1,const Mat& img2,const Mat &img3,const Mat& H1,const Mat& H2)
{
namedWindow("show",WINDOW_NORMAL);
resizeWindow("show",800,600);
Mat canvas;
/*process img1 and img2 , i.e., middle and right*/
/* adjust the H*/
Mat H = H1.clone();
for(int i = 0;i<3;++i)
{
H.at<double>(0,i) += H.at<double>(2,i)*double(img1.cols);
H.at<double>(1,i) += H.at<double>(2,i)*double(img1.rows);
}
warpPerspective(img2,canvas,H,Size(3*img2.cols,3*img2.rows));
/*process img1 and img3 , i.e., middle and left*/
H = H2.clone();
for(int i = 0;i<3;++i)
{
H.at<double>(0,i) += H.at<double>(2,i)*double(img1.cols);
H.at<double>(1,i) += H.at<double>(2,i)*double(img1.rows);
}
Mat canvas2;
warpPerspective(img3,canvas2,H,Size(3*img2.cols,3*img2.rows));
add(canvas,canvas2,canvas);
/*move the origin image to center*/
img1.convertTo(canvas(Rect(img1.cols,img1.rows,img1.cols,img1.rows)),CV_8UC3);
imshow("show",canvas);
imwrite("../stitch.jpg",canvas);
waitKey();
}
main函数过程
int main(int argc,char** argv)
{
// camera matrix
FileStorage params("../camera.yaml",FileStorage::READ);
Mat K = params["K"].mat(); // camera matrix
Mat img1 = imread("../stereo-data/0_orig.jpg");
Mat img2 = imread("../stereo-data/1_orig.jpg");
Mat H1,H2;
Mat img3 = imread("../stereo-data/2_orig.jpg");
find_Trans_H(img2,img1,H1);/*img2 project to img1*/
find_Trans_H(img3,img1,H2);/*img3 project to img1*/
process_Stitch(img1,img2,img3,H1,H2);
}
效果,拼接痕迹是难免的,这里我们主要学习$H$矩阵的运用,若想进一步详细了解图像拼接可参考《计算机视觉:算法与运用》

思考
若给出了图像对应的深度图,那么便可知道图像各点的坐标值,那么便可通过重投影的方式进行图像拼接,不妨以此来验证$E$转移矩阵的估计效果。
下面的方法,是一种恢复尺度的方式,在单目slam中,我们将各个特征点深度设为1来初始化尺度,也要估计缩放尺度。若想了解更为复杂但可靠的算法,可参考《Least-Squares Estimation of Transmation Parameters Between Two Point Patterns》
下面便为基于上面基于本质矩阵$E$单目估计相机运动方法,根据深度图来计算平移向量$t$的尺度。
1
2
3
4
5
6
7
8
9
void find_use_E(const Mat &img1,const Mat& depth1,const Mat& img2,const Mat& depth2,const Mat& K,Mat& R,Mat& t)
{
vector<Point2f> left_pts;
vector<Point2f> right_pts;
find_match(img2,img1,left_pts,right_pts);
// find the Essential Matrix using RANSAC
Mat E = findEssentialMat(left_pts,right_pts,K,RANSAC);
recoverPose(E,left_pts,right_pts,K,R,t);
在这时,$t$为归一化值,并不对应实际尺度,但我们知道$t_0 = \alpha t$,一个常见的思路便是通过最小二乘法来求解$\alpha$值,即 \(\min_\alpha \sum_i \frac{1}{2}||RP_i^i+\alpha t -P_2^i||^2\) 这显然是一个无约束凸优化问题,通过求导求得$\alpha$闭式解 \(\sum_i(RP_1^i+\alpha t+P_2^i)^Tt = 0\\ \alpha^* = \frac{1}{N\cdot ||t||^2}\sum_{i=1}^N(P_2^i-RP_1^i)^Tt\)
/*using alpha formula*/
double alpha = 0;
vector<Point2f> crpt,clpt;
/* to norm camera coordination*/
undistortPoints(left_pts,clpt,K,noArray());
undistortPoints(right_pts,crpt,K,noArray());
int N = 0;
for(int i=0;i<right_pts.size();++i)
{
Mat x1 = Mat(1,3,CV_64F);
x1.at<double>(0,0) = clpt[i].x;
x1.at<double>(0,1) = clpt[i].y;
x1.at<double>(0,2) = 1;
Mat x2 = Mat(3,1,CV_64F);
x2.at<double>(0,0) = crpt[i].x;
x2.at<double>(1,0) = crpt[i].y;
x2.at<double>(2,0) = 1;
Mat error = x1*E*x2;
/*这里通过对极约束式子的值来排除一些外点(outlier)*/
if(abs(error.at<double>(0,0))<MIN_ERROR) {
Mat result = ((depth1.at<float>(right_pts[i].y,right_pts[i].x)*x2) - R*(depth2.at<float>(left_pts[i].y,left_pts[i].x)*x1).t()).t()*t;
alpha += result.at<double>(0,0);
++N;
}
}
alpha = alpha/N/t.dot(t);
t = alpha*t;
下面即为计算反投影误差
vector<Point2f> cp2;
undistortPoints(left_pts,cp2,K,noArray());
vector<Point3f> cp2_;
/*reproject to 3D*/
for(int i=0;i<left_pts.size();++i)
{
float d = depth2.at<float>(left_pts[i].y,left_pts[i].x);
cp2[i]*=d;
cp2_.emplace_back(cp2[i].x,cp2[i].y,d);
}
Mat rvec;
Rodrigues(R,rvec);
vector<Point2f> check;
projectPoints(cp2_,rvec,t,K,noArray(),check);
double error = 0;
for(int i = 0;i<check.size();++i)
{
error += norm((check[i]-right_pts[i]));
}
error /= check.size();
printf("E error is %.3f\n",error);
}
此外,我们根据特征点来做PNP,与用$E$求解的做对比
void find_PnP(const Mat& img1,const Mat& depth1,const Mat& img2,const Mat& depth2,const Mat& K,Mat &rvec,Mat &tvec)
{
vector<Point2f> lpt,rpt;
find_match(img1,img2,lpt,rpt);
vector<Point2f> cp2;
undistortPoints(rpt,cp2,K,noArray());
vector<Point3f> cp2_;
对第二张图片视角,根据深度图计算其相机坐标系坐标(作为世界坐标),然后对对应点做SolvePnPRansac,做Ransac的原因是匹配可能有外点(outlier)
然后计算重投影误差
/*reproject to 3D*/
for(int i=0;i<rpt.size();++i)
{
float d = depth2.at<float>(int(rpt[i].y),int(rpt[i].x));
cp2[i]*=d;
cp2_.emplace_back(cp2[i].x,cp2[i].y,d);
}
solvePnPRansac(cp2_,lpt,K,noArray(),rvec,tvec);/*from img2 to img1*/
vector<Point2f> check;
projectPoints(cp2_,rvec,tvec,K,noArray(),check);
double error = 0;
for(int i = 0;i<check.size();++i)
{
error += norm((check[i]-lpt[i]));
}
error/=check.size();
printf("pnp error is %.3f\n",error);
}
结果,PnP的效果较好,但对于$E$矩阵估计我们使用了较为基本的估计算法,也达到了不错的恢复尺度的效果
1
2
pnp error is 10.423
E error is 14.169
下面便利用两种方法估计的位姿进行重投影
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void process_Stitch_project(const Mat &img1,const Mat& depth1,const Mat& img2,const Mat& depth2,const Mat& K,const Mat& R,const Mat& tvec,char* mask)
{
char title[50];
sprintf(title,"project_%s",mask);
namedWindow(title,WINDOW_NORMAL);
resizeWindow(title,800,600);
/* from img2 to img1*/
Mat rvec;
Rodrigues(R,rvec);
vector<Point2f> ip2;
vector<Point2f> cp2_norm;/*x0,y0 on normal camera coordination*/
vector<Point3f> cp2;
以下为计算第二张图片各点在第二个相机坐标系下的坐标值,经历了转换到归一化相机坐标系再乘上深度值的过程
for(int i = 0;i<img2.rows;++i)
for(int j = 0;j<img2.cols;++j)
ip2.emplace_back(j,i);
undistortPoints(ip2,cp2_norm,K,noArray());
for(int i = 0;i<img2.rows;++i)
for(int j = 0;j<img2.cols;++j)
{
float d = depth2.at<float>(i,j);
cp2.emplace_back(cp2_norm[i*img2.cols+j].x*d,cp2_norm[i*img2.cols+j].y*d,d);
}
根据输入的从第二个相机坐标系到第一个相机坐标系的变换关系进行重投影
vector<Point2f> project_ps2;
projectPoints(cp2,rvec,tvec,K,noArray(),project_ps2);
Mat canvas = Mat::zeros(3*img1.rows,3*img1.cols,CV_8UC3);
进行重投影RGB信息,将重投影点对应的原来图像位置的RGB值复制到新投影位置
img1.convertTo(canvas(Rect(img1.cols,img1.rows,img1.cols,img1.rows)),CV_8UC3);
for(int i = 0;i<img2.rows;++i)
{
for(int j = 0;j<img2.cols;++j)
{
canvas.at<Vec3b>(cvRound(project_ps2[i*img2.cols+j].y)+img1.rows,cvRound(project_ps2[i*img2.cols+j].x)+img1.cols) = img2.at<Vec3b>(i,j);
}
}
imshow(title,canvas);
waitKey();
sprintf(title,"../project_%s.jpg",mask);
imwrite(title,canvas);
}
下面是效果,由于重投影图片过暗,该效果是重投影像素RGB值均乘2的效果
PnP估计效果

E估计效果

双目视觉
双目视觉的基本模型和极线约束是相同的,只不过在双目视觉中,两个相机之间的位姿关系是已知的(标定出来)。
我们先来看一下双目相机如何标定。更为详细的标定,可参考opencv_$version$/samples/cpp/stereo_calib.cpp
先如同单目标定,读入图片,找角点
#define N 21
#define quad 69
#define H 6
#define W 9
int main(int argc,char** argv)
{
namedWindow("check",WINDOW_NORMAL);
resizeWindow("check",800,600);
// read the single camera param
FileStorage camera("../stereo.yaml",FileStorage::READ);
Mat K_0 = camera["K_0"].mat();
Mat C_0 = camera["C_0"].mat();
Mat K_1 = camera["K_1"].mat();
Mat C_1 = camera["C_1"].mat();
//read the calibrate data
char filename[50];
vector<Mat> left_im,right_im;
vector<vector<Point2f>> corners_vec_left,corners_vec_right;
sprintf(filename,"../left/%d_l.jpg",1);
Mat tmp = imread(filename);
/* img Size*/
Size im_size(tmp.cols,tmp.rows);
/*generate object points*/
vector<vector<Point3f>> object;
for(int i = 1;i<=N;++i)
{
if(i==12)continue; /* 12 not exist*/
Mat img;
vector<Point2f> corners;
sprintf(filename,"../left/%d_l.jpg",i);
img = imread(filename);
Mat gray;
cvtColor(img,gray,COLOR_BGR2GRAY);
left_im.push_back(img.clone());
findChessboardCorners(gray,Size(W,H),corners);
find4QuadCornerSubpix(gray,corners,Size(5,5));
drawChessboardCorners(img,Size(W,H),corners,true);
corners_vec_left.push_back(corners);
imshow("check",img);
waitKey(10);
sprintf(filename,"../right/%d_r.jpg",i);
img = imread(filename);
cvtColor(img,gray,COLOR_BGR2GRAY);
right_im.push_back(img.clone());
findChessboardCorners(gray,Size(W,H),corners);
find4QuadCornerSubpix(gray,corners,Size(5,5));
drawChessboardCorners(img,Size(W,H),corners,true);
corners_vec_right.push_back(corners);
imshow("check",img);
waitKey(10);
vector<Point3f> object_per_im;
/* rows to cols*/
for(int j = 0;j<H;++j)for(int k = 0;k<W;++k)object_per_im.emplace_back(k*quad,j*quad,0);
object.push_back(object_per_im);
}
然后进行双目标定,这里得到参数我们都很熟悉,$R,t,E,F$都在我们上面的讲解中出现,实际上你还可以用对极约束来验证这一过程。
Mat R,t,E,F;
double rms = stereoCalibrate(object,corners_vec_left,corners_vec_right,K_0,C_0,K_1,C_1,im_size,R,t,E,F);
cout<<"rms is "<<rms<<endl;
然后我们要做双目立体矫正,这是一个比较复杂的过程,但下面的图片十分清晰地解释了该过程
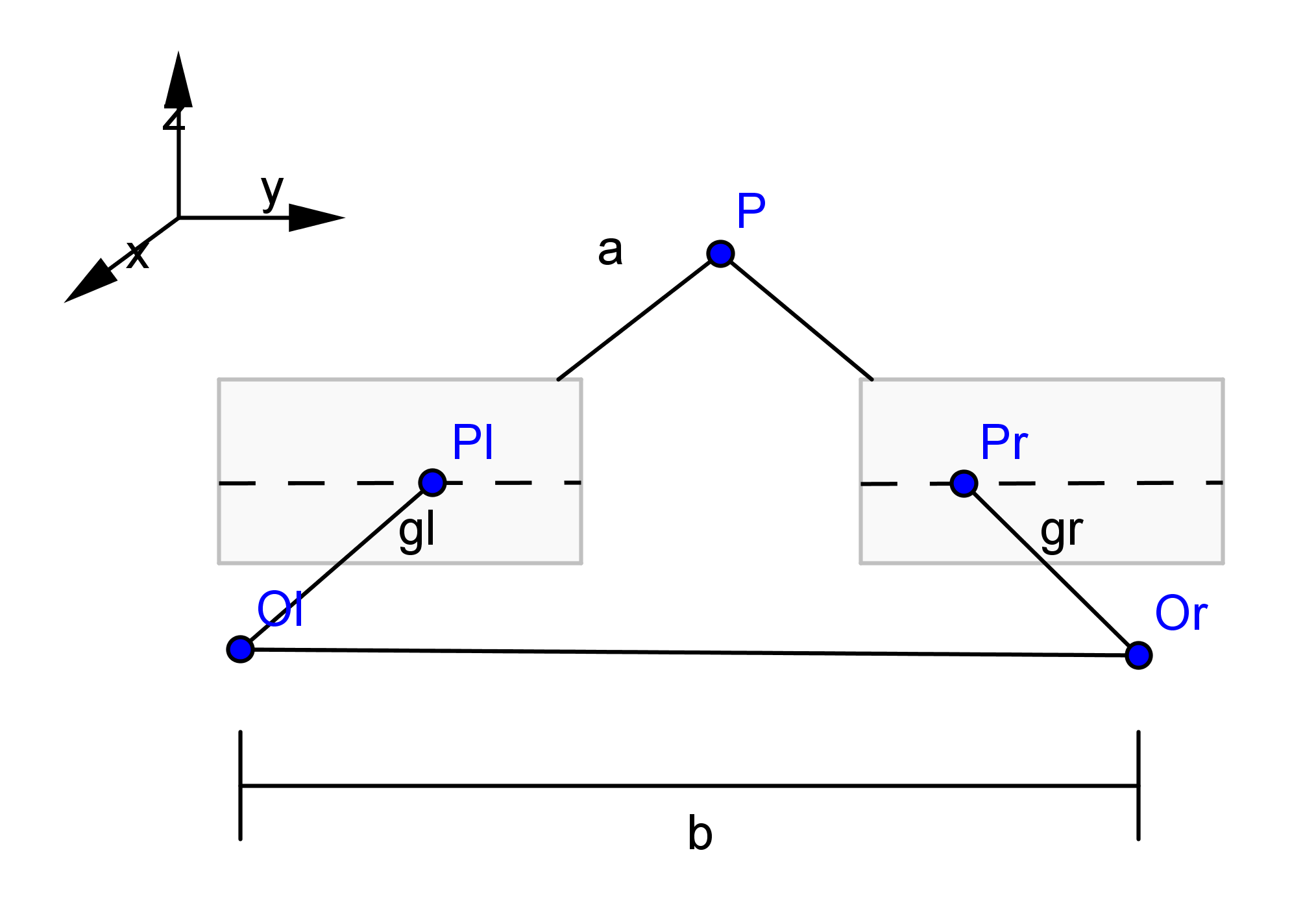
stereoRectify函数输出了$R_1,R_2,P_1,P_2,Q$
来自官方文档的解析
$R_1$
1
Output 3x3 rectification transform (rotation matrix) for the first camera. This matrix brings points given in the unrectified first camera's coordinate system to points in the rectified first camera's coordinate system. In more technical terms, it performs a change of basis from the unrectified first camera's coordinate system to the rectified first camera's coordinate system.
实际上就是左相机未矫正坐标系旋转到矫正坐标系的旋转矩阵,如上图,$R2$同理
$P_1$
1
Output 3x4 projection matrix in the new (rectified) coordinate systems for the first camera, i.e. it projects points given in the rectified first camera coordinate system into the rectified first camera's image.
实际上就是一个$3\times 4$矩阵,矫正(rectified)相机坐标系投影到矫正左像素平面的变换矩阵(外参+内参),$P_2$是矫正(rectified)相机坐标系投影到矫正右像素平面的变换矩阵。 $$ P_1 = \left[ \begin{matrix}f& 0 & c_x & 0\0 & f& c_y & 0\0& 0& 1 & 0 \end{matrix}\right]\
P_2 = \left[ \begin{matrix}f& 0 & c_x & T_x\cdot f\0 & f& c_y & 0\0& 0& 1 & 0 \end{matrix}\right] = \left[ \begin{matrix}f& 0 & c_x \0 & f& c_y \0& 0& 1 \end{matrix}\right]\left[ \begin{matrix}1& 0 & 0 & T_x\0 & 1& 0 & 0\0& 0& 1 & 0 \end{matrix}\right] $$ 以上为横向双目(Horizontal stereo)的模型,$T_x\cdot f$是X轴向平移,从上面图可以看出,两个旋转矫正后的平面之间是有X轴向位移的。
$P$矩阵的前三列是旋转矫正后的新的相机内参。
$Q$
1
Output 4×4 disparity-to-depth mapping matrix (see reprojectImageTo3D).
顾名思义,从视差到深度映射矩阵,在reprojectImageTo3D这个函数我们暂时不会介绍,在进行稠密深度估计中,我们会得到视差图,通过该函数我们将视差图变换为深度图。
Mat R1,P1,R2,P2,Q;
stereoRectify(K_0,C_0,K_1,C_1,im_size,R,t,R1,R2,P1,P2,Q);
FileStorage fs;
fs.open("../extrinsics.yml", FileStorage::WRITE);
fs << "R" << R << "T" << t << "E"<<E<<"F"<<F<<"R1" << R1 << "R2" << R2 << "P1" << P1 << "P2" << P2 << "Q" << Q;
fs.release();
Mat map1_l,map2_l;
我们通过initUndistortRectifyMap计算两个相机坐标系之间的映射,并对每一张标定图片进行极线矫正,并查看效果
initUndistortRectifyMap(K_0,C_0,R1,P1,im_size,CV_16SC2,map1_l,map2_l);
Mat map1_r,map2_r;
initUndistortRectifyMap(K_1,C_1,R2,P2,im_size,CV_16SC2,map1_r,map2_r);
for(int i = 0;i<left_im.size();++i)
{
Mat r1,r2;
remap(left_im[i],r1,map1_l,map2_l,INTER_AREA);
remap(right_im[i],r2,map1_r,map2_r,INTER_AREA);
Mat canvas = Mat(left_im[0].rows,left_im[0].cols*2,CV_8UC3);
r1.convertTo(canvas(Rect(0,0,im_size.width,im_size.height)),CV_8UC3);
r2.convertTo(canvas(Rect(im_size.width,0,im_size.width,im_size.height)),CV_8UC3);
for(int j = 0;j<32;++j)line(canvas,Point(0,j*canvas.rows/33+10),
Point(canvas.cols-1,j*canvas.rows/33+10),Scalar(0,255,0),2);
imshow("check",canvas);
if(i == 0)imwrite("../ref.jpg",canvas);
waitKey();
}
return 0;
}

以上是极线矫正后的样子,可见大部分对应点都落在了同一条直线上。

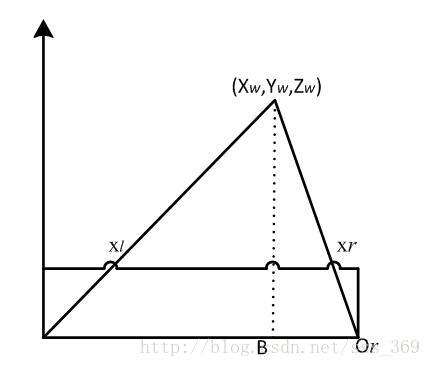
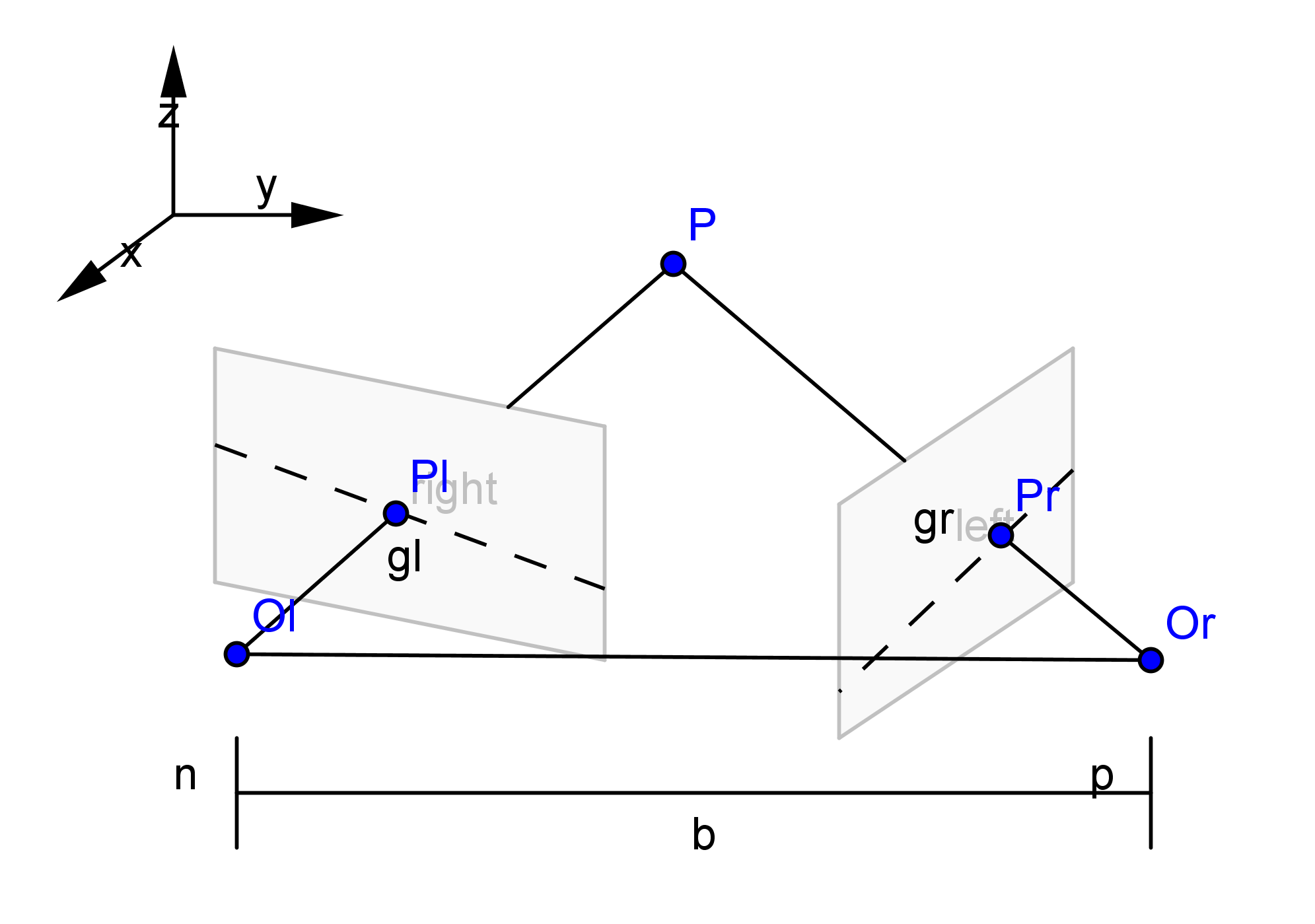
双目中另一个比较重要的概念是三角测量,其原理十分简单,对于极线矫正后的两个归一化相机平面,有 \(\frac{z-f}{z} = \frac{b-x_L+x_R}{b}\\ \frac{f}{z} = \frac{x_L-x_R}{b}=\frac{d}{b}\\ z =\frac{f\cdot b}{d}\) 最后一个公式即为三角测量公式,请牢记于心。其中$d$称为视差,$b$称为基线。
实际上在opencv中,上述公式一般用于估计稠密深度图中,视差图到深度图的转换。而在直接的三角测量函数,一般使用如下公式 \(z_1 x_1 = z_2Rx_2+t\\ x_1\times z_1 x_1 = 0=z_2x_1\times Rx_2 + x_1\times t\\ z_2(x_1^{\ \hat{}} Rx_2) = -x_1^{\ \hat{}} t\) 考虑到噪声,我们应该求解该式的最小二乘解来得到$z_2$,求得$z_2$自然也容易得到$z_1$。
上述公式都说明了在三角测量中需要用到齐次相机坐标。
在opencv中的三角测量函数是triangulatePoints
| projMatr1 |
|---|
| 3x4 从世界坐标系到第一个相机的变换矩阵(通常我们使得第一个相机为世界坐标系,则该项为单位阵去除最后一行) |
| projMatr2 |
| 3x4 从世界坐标系到第二个相机的变换矩阵(若使用上述方案,则该项为[R,t],则双目相机标定中, $R,t$均为从左相机到右相机的变换) |
| projPoints1 |
| 第一张图片中点在归一化相机平面上的坐标,建议用vector<Point2f>,该函数不接受double类型 |
| projPoints2 |
| 第二张图片中点在归一化相机平面上的坐标,建议用vector<Point2f>,该函数不接受double类型 |
| points4D |
| 输出,一般用Mat接受,是一个4xN矩阵,每一列为一个输出的在世界坐标系下的点 需要除以第四位来归一化 |
这个函数的使用作为作业的一部分,这里给出一部分作业代码用作该函数使用样例
/*create translation Matrix*/
Mat T1 = Mat::eye(3,4,CV_64F);
Mat T2 = Mat(3,4,CV_64F);
R.convertTo(T2(Rect(0,0,3,3)),CV_64F);
T.convertTo(T2(Rect(3,0,1,3)),CV_64F);
/* 变换到归一化相机坐标系*/
vector<Point2f> undistort_lpts,undistort_rpts;
undistortPoints(lpts,undistort_lpts,K_0,C_0);
undistortPoints(rpts,undistort_rpts,K_1,C_1);
Mat results;
triangulatePoints(T1,T2,undistort_lpts,undistort_rpts,results);
/* results is a 4*N matrix*/
for(int i = 0;i<results.cols;++i)
{
float D = results.at<float>(3,i);
/* 通过归一化,得到第一个相机坐标系下各点坐标*/
Point3f p_3d(results.at<float>(0,i)/D,results.at<float>(1,i)/D,results.at<float>(2,i)/D);
}
作业
给出一对由双目相机拍摄的视频,在视频开始时在左目相机中选择一个ROI框,然后估计该ROI中心点在每一帧的实时深度(左相机坐标系下z轴值)。
Hint
- 这个作业里,你需要用到特征点匹配,但不一定要用到极线搜索的知识,我们建议直接对框中区域内部图像计算特征点,然后对另外一目图像全局寻找特征点,通过暴力匹配或者FLANN匹配的方式来匹配特征点。当你找到匹配的较好特征点后,进行三角测量测距,并对所有特征点的深度(即z坐标)进行平均,然后输出深度在视频里。
- 两个相机之间的位姿关系可以通过上述的双目标定得到,在给出的数据中,提供了标定好的外参,基于此,你甚至可以通过对极约束来排除误匹配的特征点来得到较好的匹配点
- 你也可以学习计算稠密深度图来直接得到稠密的深度信息,OpenCV提供这样的检测器,实际上它就用到了极线搜索的方法
作业效果示例:

Application
- 做完了这个项目,你应该对于双目立体视觉系统有了了解,在比赛中,双目系统可以用在雷达系统,以及哨兵反导等项目中。
这里简单介绍一下极线搜索
仍然是这张图片,在大部分情况下,我们很难知道$P_r$的位置,但是通过极线矫正,我们知道它一定在$P_l$所在的极线上,那么我们只要搜索这条极线便可。
三角测量的局限
我们在使用双目系统进行测距时,应该注意到
- 较大的基线长度,会使得在同样的匹配误差下,相对的深度误差较小
- 同样的基线长度,目标距离越远,在同样的匹配误差下,相对的深度误差就会越大
由于我们并不能使用很长基线的双目系统(特别是在车上),故而双目系统一般用在较近距离(如10m内)的测距,较远距离将会带来难以接受的误差。
光流
光流根据了灰度不变假设,即对于连续两帧图片,若定义$I(x,y,t)$为$t$时刻下$(x,y)$位置的像素的灰度(gray-level),则有假设 \(I(x,y,t) = I(x+\delta x,y+\delta y,t+\delta t)\) 对右边项进行泰勒展开一阶项 \(I(x,y,t) \approx I(x,y,t) + \frac{\part I}{\part x}\delta x+ \frac{\part I}{\part y}\delta y+\frac{\part I}{\part t}\delta t\\ \frac{\part I}{\part x}\frac{\delta x}{\delta t}+\frac{\part I}{\part y}\frac{\delta y}{\delta t} = -\frac{\part I}{\part t}\\ \left[\begin{matrix}\frac{\part I}{\part x}&\frac{\part I}{\part y}\end{matrix}\right]\left[\begin{matrix}\frac{\delta x}{\delta t}\\\frac{\delta y}{\delta t}\end{matrix}\right] = -\frac{\part I}{\part t}\) 若我们取相邻帧,$\delta t = 1$,则有 \(\left[\begin{matrix}\frac{\part I}{\part x}&\frac{\part I}{\part y}\end{matrix}\right]\left[\begin{matrix}\delta x\\\delta y\end{matrix}\right] = -\frac{\part I}{\part t}\) 类似上面的做法,我们假设一个$w \times w$的方格内像素具有相同的运动,则可得一个线性方程组,解线性方程便可得得到像素运动。
下面便是实践时间,我们来看一个视频上各个特征点根据光流法追踪的效果。
int main(int argc,char** argv)
{
if(argc < 3){cerr<<"input infile and outfile!"<<endl;return -1;}
namedWindow("show",WINDOW_NORMAL);
resizeWindow("show",800,600);
VideoCapture cap(argv[1]);
if(!cap.isOpened()) {cerr << "no such file!"<<endl;
cap.release();
return -1;}
Ptr<ORB> orb = ORB::create(1700);
bool flag;
Mat frame;
flag = cap.read(frame);
VideoWriter writer(argv[2],VideoWriter::fourcc('m','p','4','v'),10.,Size(frame.cols,frame.rows));
用orb计算特征点,这里只需要计算特征点,而不需要计算描述子
1
2
3
4
5
6
7
8
9
10
11
Mat gray;
cvtColor(frame,gray,COLOR_BGR2GRAY);
// create the container of Key points
vector<KeyPoint> feature_points;
// do Orient_FAST detect Keypoint
orb->detect(gray,feature_points);
vector<Point2f> prev_pts,now_pts;
for(const KeyPoint& p : feature_points)
{
prev_pts.push_back(p.pt);
}
calcOPticalFLowPyrLK利用LK光流算法计算光流,其中参数,prev是上一帧图像,frame是这一帧图像,都是彩色图像输入,prev_pts是上帧预计算的点,now_pts是这一帧输出的点,status存储了now_pts中该点是否为正确估计,error存储了正确的点估计的误差
Mat prev;
vector<float> error; /* error of each found corresponding points*/
vector<unsigned char> status; /* to show whether the corresponding point in the next frame is found or not.*/
while(true)
{
prev = frame.clone();
flag = cap.read(frame);
if(!flag)break;
calcOpticalFlowPyrLK(prev,frame,prev_pts,now_pts,status,error);
Mat canvas = frame.clone();
int i=0;
int iter = 0;
for(auto p:prev_pts)
{
/* prev pt*/
circle(canvas,Point2i(cvRound(p.x),cvRound(p.y)),2,Scalar(0,255,0),-1);
if(status[i++]==0) {
now_pts.erase(now_pts.begin()+iter);
continue;
}
int x = cvRound(now_pts[iter].x);
int y = cvRound(now_pts[iter].y);
circle(canvas,Point2i(x,y),
2,Scalar(0,0,255),-1);
line(canvas,Point2i(cvRound(p.x),cvRound(p.y)),
Point2i(cvRound(now_pts[iter].x),cvRound(now_pts[iter].y)),
Scalar(0,255,0));
++iter;
}
if(now_pts.size()==0)
break;
char count[50];
sprintf(count,"reserve from %d to %d",int(prev_pts.size()),int(now_pts.size()));
putText(canvas,count,Point(100,100),FONT_HERSHEY_COMPLEX,1,Scalar(0,255,0));
prev_pts.clear();
prev_pts = now_pts;
imshow("show",canvas);
writer.write(canvas);
waitKey(80);
}
writer.release();
cap.release();
}
进阶读物
该博客对基于opencv传统双目视觉做了进一步的讲解和实践,并涉及到利用opencv工具建立稠密深度图,并进行深度补全,若对该方面感兴趣,可在本讲基础上对该博客代码进行实践。
《视觉slam十四讲:从理论到实践》第9讲:实践,设计前端
基于该讲与前面所学,你已经对于一个相机的模型有了充分的认识,并且如何建模与估计相机的运动也有了了解,很显然,你已经具备了制作一个视觉里程计的基本知识,这将是一个复杂系统,使得你用到前面所学的各种知识
如果觉得本教程不错或对您有用,请前往项目地址 https://github.com/Harry-hhj/Harry-hhj.github.io 点击 Star :) ,这将是对我的肯定和鼓励,谢谢!
Acknowledgement
- 本教程大部分参考自《视觉slam十四讲》
- 图片大部分来自CSDN,博客园等
- 少数摘自OpenCV文档,OpenCV文档yyds
作者:郑煜,github主页:传送门