RM 教程 5 —— 单目视觉

机械是肉体，电控是大脑，视觉是灵魂

一、仿射变换与透视变换

0. 再谈其次坐标系

在上一讲中，我们提到了齐次坐标系。对于二维平面上的点 $(x, y)$ ，我们常常将它写成为 $(x, y, 1)^{T}$ ，这是一个典型的齐次坐标。同样的，在三维空间中，我们有坐标 $(x, y, z, 1)^{T}$ ，这也是一个齐次坐标形式。

显然，对于齐次坐标和非齐次坐标，我们可以简单地通过删除最后一个坐标 $1$ 来实现他们之间的转换。但这样看来，齐次坐标的表述仍然非常奇怪，因为它多了一个莫名其妙的限制，就是最后一个坐标数值一定为 $1$ 。那么一个坐标三元组 $(x, y, 2)^{T}$ 是否也有自己的意义呢?

对此，我们规定对于任何非零值 $k$ ， $(k x, k y, k)^{T}$ 表示二维坐标中的同一个点，也就是说，当两个三元组相差一个公共倍数时，他们是等价的，也被成为坐标三元组中的等价类。

现在问题有出现了，在上面的定义中，我们规定 $k \neq 0$ ，那么当 $k = 0$ 时，坐标三元组 $(x, y, 0)^{T}$ 是否有它的意义?

由于 $(x / 0, y / 0)^{T}$ 得到的应该是一个在无穷远方的点，因此我们称它为无穷远点。在二维空间中，无穷远点形成无穷远直线。在三维中，他们形成无穷远平面。

1. 线性变换

在谈仿射变换之前，我们先要复习一下线性变换。

线性变换从几何直观有三个要点：

变换前是直线的，变换后依然是直线
直线比例保持不变
变换前是原点的，变换后依然是原点

线性变换是通过矩阵乘法来实现的。

1. 仿射变换

仿射变换是一种特殊的坐标变换，在仿射变换下，形状的两个平行性和体积比保持不变。

如果从无穷远直线的角度理解仿射变换，那么：假设在空间 $s$ 下直线 $l$ 为无穷远直线，当经过仿射变换 $A$ 后得到直线 $l^{'}$ ， $l^{'}$ 仍然为仿射变换后的空间 $s^{'}$ 中的无穷远直线。

仿射变换的公式为： $[\begin{matrix} x^{'} \\ y^{'} \\ 1 \end{matrix}] = [\begin{matrix} A & t \\ 0^{T} & 1 \end{matrix}] [\begin{matrix} x \\ y \\ 1 \end{matrix}]$ 如果上述的表达方式太过数学化，我们可以用直观的方式帮助你理解仿射变换：

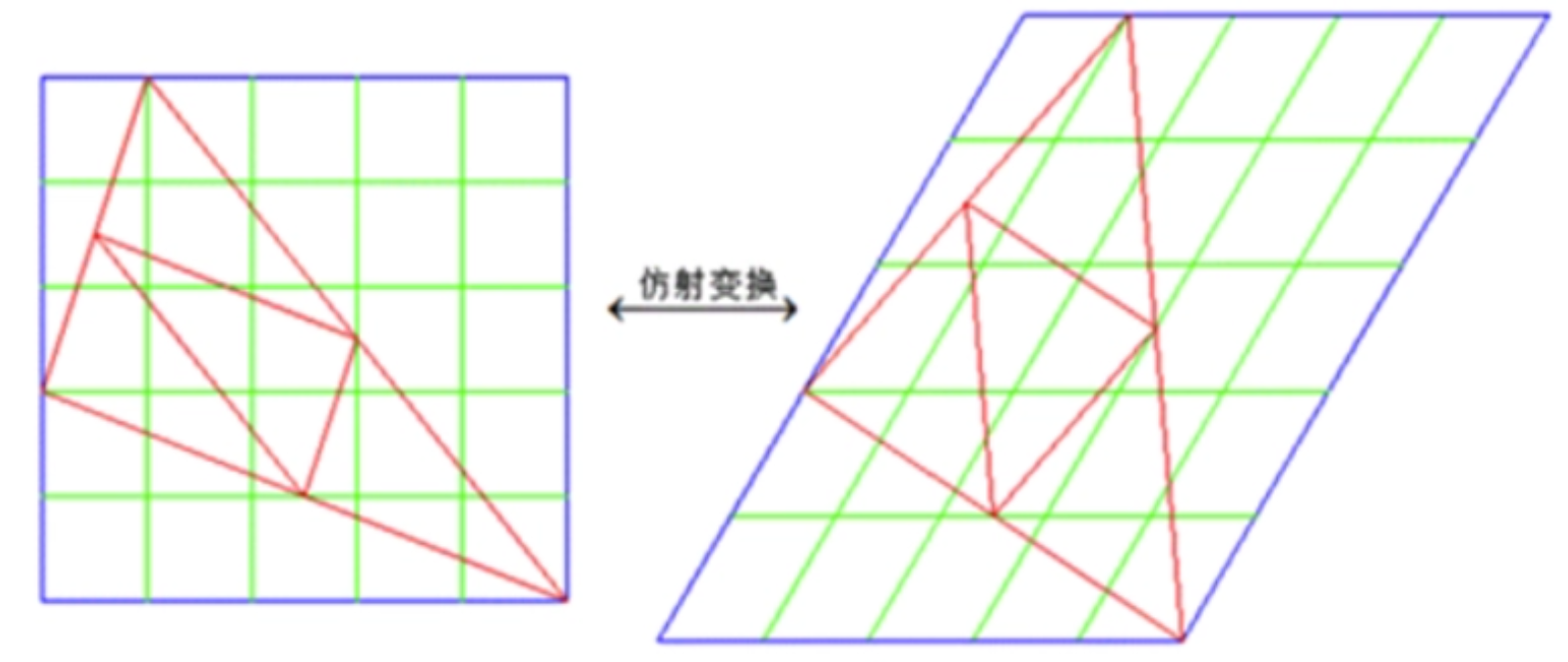
对于仿射变换的感性理解就是，将输入图像想象为一个大的矩形橡胶片，然后通过在角上的推或拉变形来制作不同样子的平行四边形。

简单来说，“仿射变换”就是：“线性变换”+“平移”。

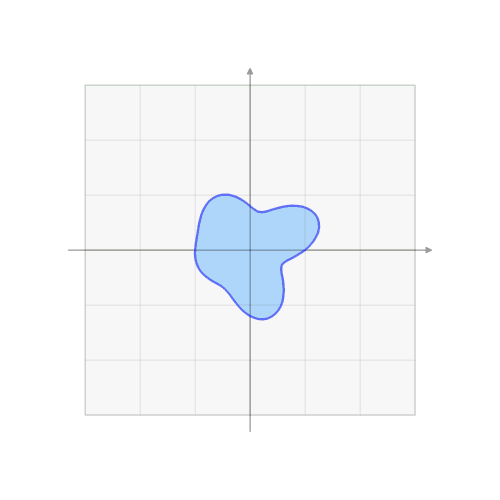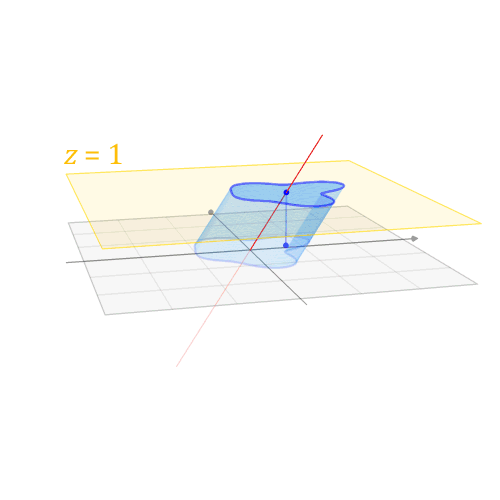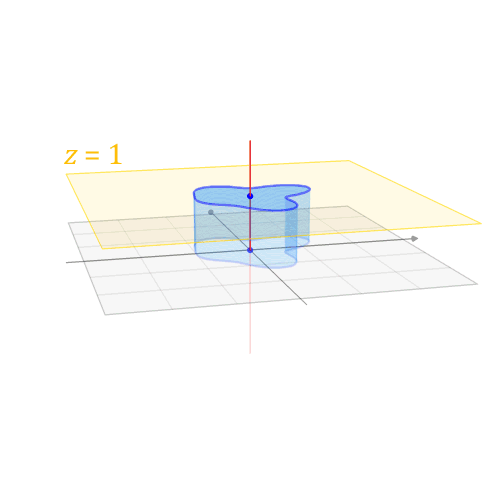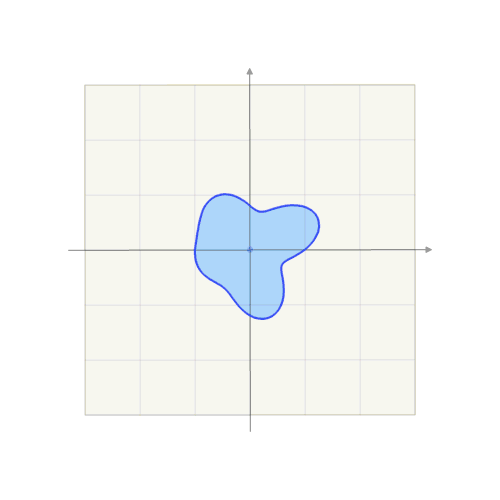
仿射变换的不变性：

线共点、点共线的关系不变
平行关系
中点
在一条直线上的几段线段的比例关系

仿射变换会改变：

线段长度
夹角角度

对于二维空间中的仿射变换，他有透视变换 $6$ 个自由度（参数），对于三维空间中的仿射变换，他有 $12$ 个自由度。

补充知识

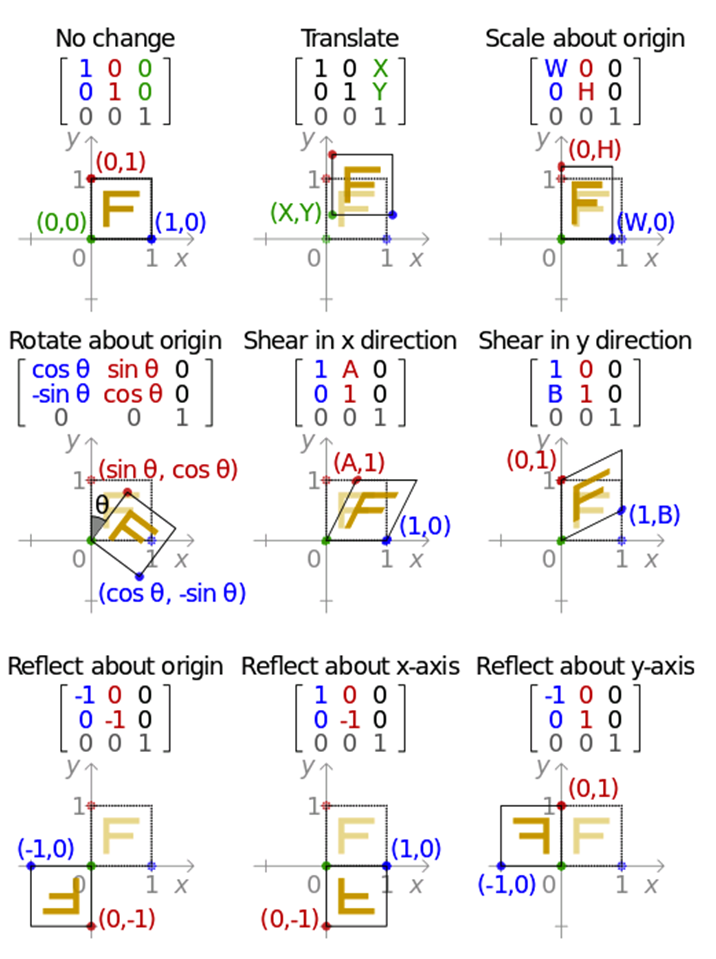
仿射变换可以通过一系列的原子变换的复合来实现，包括：平移（Translation）、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切（Shear）。理解这些特殊的变换对你理解仿射变换有一些帮助。

我们介绍一下几种常见的特殊的仿射变换：

平移变换 Translation

平移变换是一种“刚体变换”，不会产生形变的理想物体。变换矩阵为： $[\begin{matrix} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{matrix}]$

缩放变换 Scale

将每一点的横坐标放大（缩小）至 $s_{x}$ 倍，纵坐标放大（缩小）至 $s_{y}$ 倍。变换矩阵为： $[\begin{matrix} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & 1 \end{matrix}]$

剪切变换 Shear

相当于一个横向剪切与一个纵向剪切的复合。变换矩阵为： $[\begin{matrix} 1 & s h_{x} & 0 \\ s h_{y} & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] = [\begin{matrix} 1 & 0 & 0 \\ s h_{y} & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} 1 & s h_{x} & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}]$

旋转变换 Rotation

目标图形围绕原点顺时针旋转 $θ$ 弧度。变换矩阵为： $[\begin{matrix} \cos (θ) & - \sin (θ) & 0 \\ \sin (θ) & \cos (θ) & 0 \\ 0 & 0 & 1 \end{matrix}]$

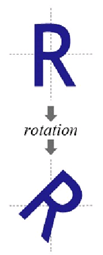
组合

旋转变换，目标图形以 $(x, y)$ 为轴心顺时针旋转 $θ$ 弧度，相当于两次平移变换与一次原点旋转变换的复合：先移动到中心节点，然后旋转，然后再移动回去。变换矩阵为： $[\begin{matrix} \cos (θ) & - \sin (θ) & y - x \cos (θ) + y \sin (θ) \\ \sin (θ) & \cos (θ) & y - x \sin (θ) - y \cos (θ) \\ 0 & 0 & 1 \end{matrix}] = [\begin{matrix} 1 & 0 & - x \\ 0 & 1 & - y \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} \cos (θ) & - \sin (θ) & 0 \\ \sin (θ) & \cos (θ) & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} 1 & 0 & x \\ 0 & 1 & y \\ 0 & 0 & 1 \end{matrix}]$

这个转换矩阵也可以下面这样描述。

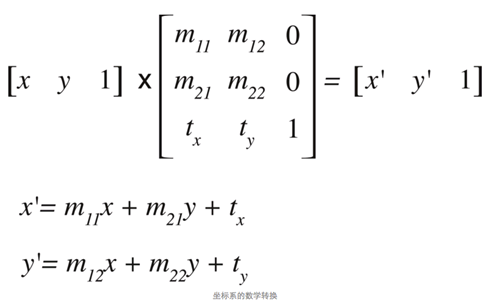
一些常用转换矩阵如下：

2. 透视变换

仿射变换可以理解为透视变换的特殊形式。透视变换也叫投影变换。我们在仿射变换中提到，通过仿射变换，原图像中的无穷远线不变。与之相反，通过透视变换，原来的无穷远线不再是无穷远线。也就是说，对于一点 $(x, y, 0)^{T}$ ，它经过透视变换之后的坐标最后一元不再为零。

透视变换不再保证平行性。

在二维空间中，空间变换的一般形式公式如下： $[\begin{matrix} x^{'} \\ y^{'} \\ k^{'} \end{matrix}] = [\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix}] [\begin{matrix} x \\ y \\ k \end{matrix}]$ 如果想通过这样的一个变换使得变换结果中的 $k^{'} \neq 0$ ，那么就必须满足 $a_{31} x + a_{32} y \neq 0$ 。

于是，我们自然而然地得到了透视变换的一般形式： $[\begin{matrix} x^{'} \\ y^{'} \\ k^{'} \end{matrix}] = [\begin{matrix} A & t \\ a^{T} & v \end{matrix}] [\begin{matrix} x \\ y \\ k \end{matrix}]$ 如果想要感性地理解透视变换，那么你可以想想从不同角度看同一个物体的效果。例如下图就是一个透视变换的示意图：

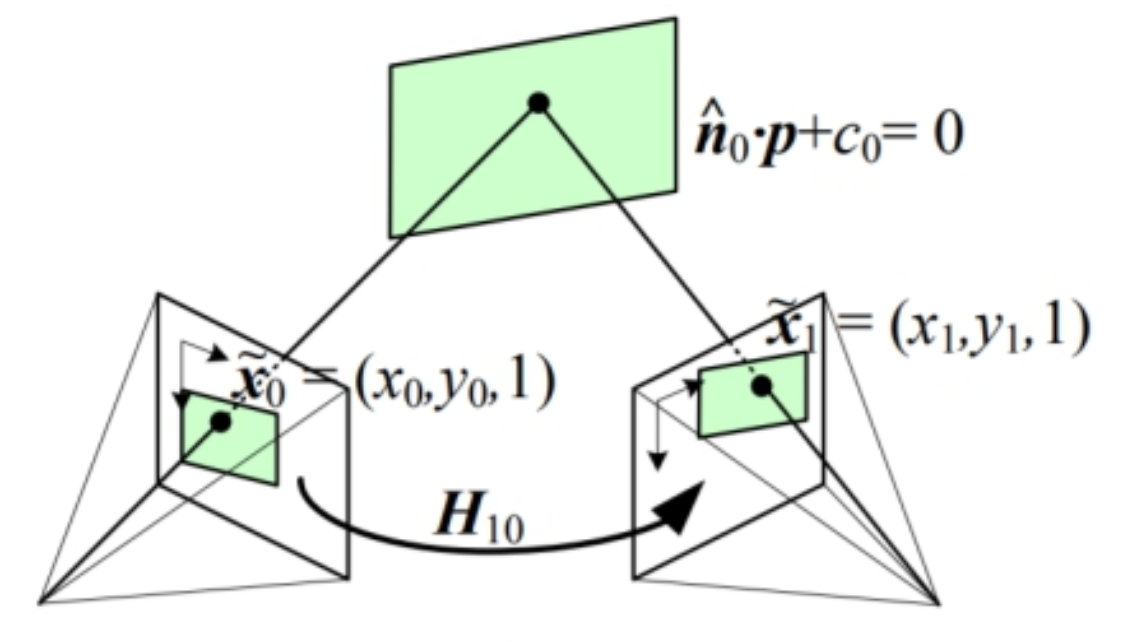
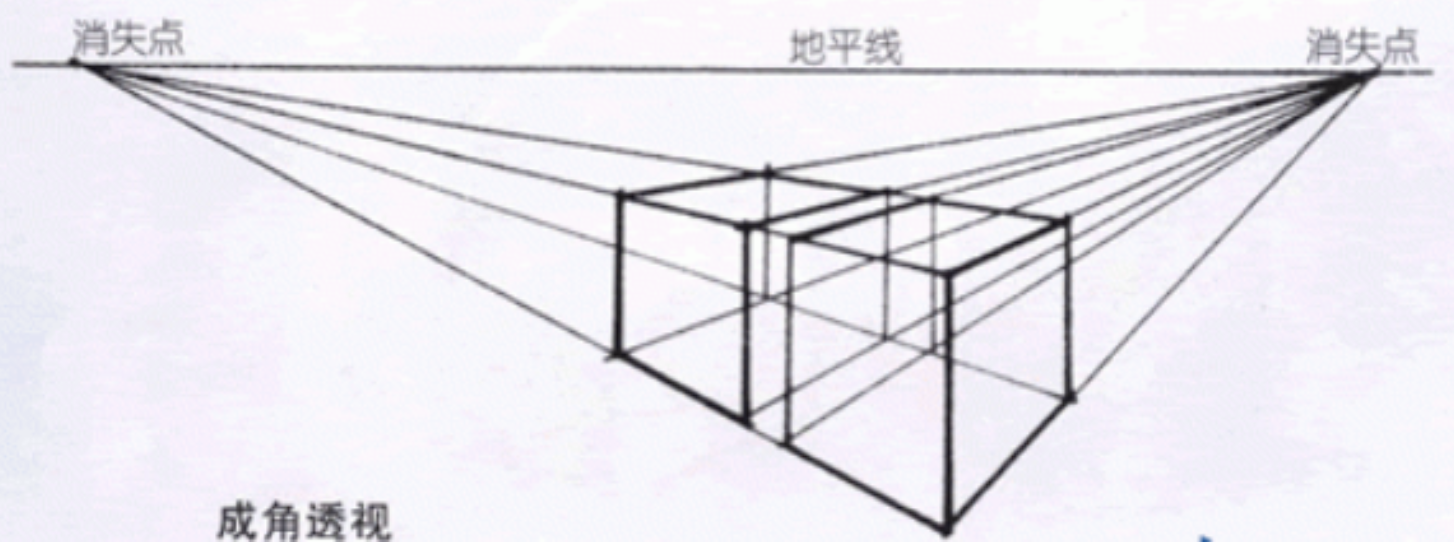
通过透视变换，我们可以转换原图的视角。

例如下图中，我们就将车道从平视图转换为俯视图：

下图中我们将车牌从侧视图转换为正视图：

对于二维空间中的透视变换，它有 $8$ 个自由度，对于三维空间中的透视变换，它有 $15$ 个自由度。

3. OpenCV中的仿射变换和透视变换

在应用层面，仿射变换是图像基于 $3$ 个固定顶点的变换，如图所示：

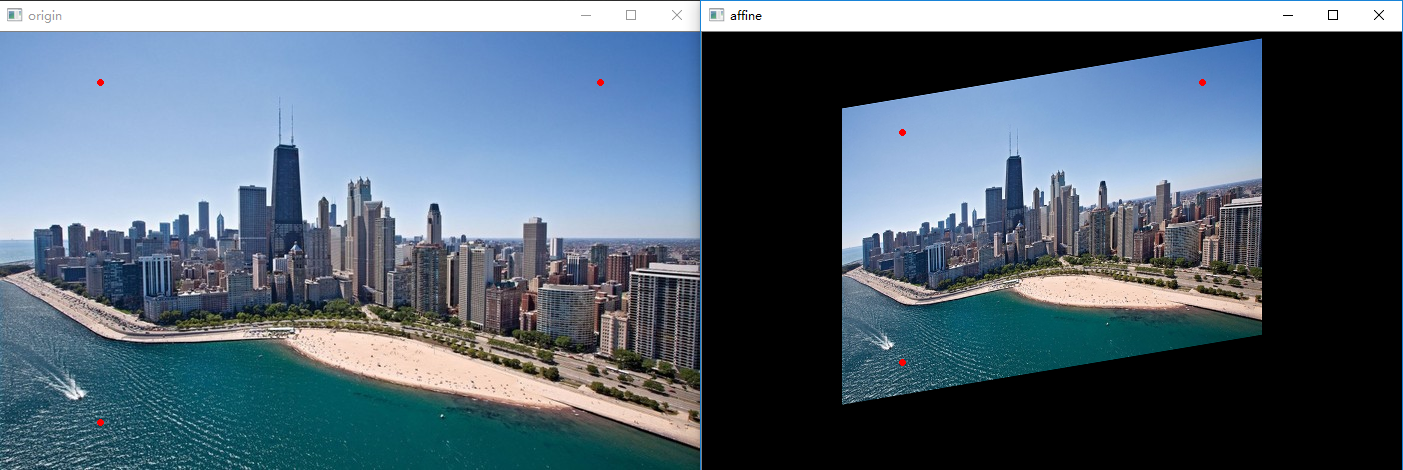
图中红点即为固定顶点，在变换先后固定顶点的像素值不变，图像整体则根据变换规则进行变换。

同理，透视变换是图像基于 $4$ 个固定顶点的变换，如图所示：

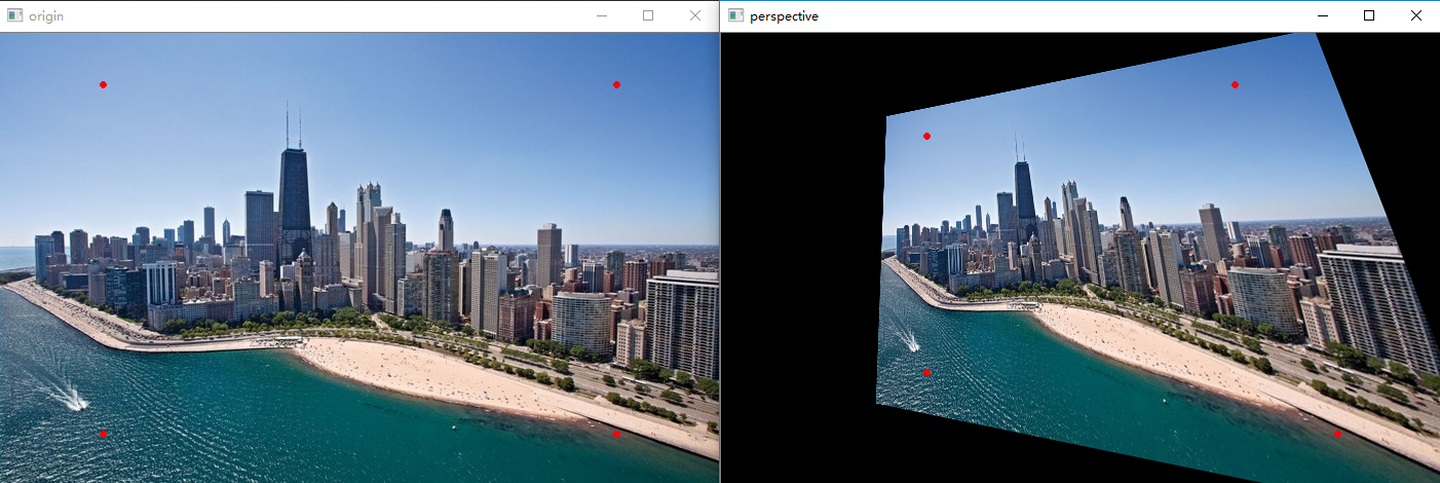
在OpenCV中，仿射变换和透视变换均有封装好的函数。

仿射变换的函数是：

  
void cv::warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

参数：

InputArray src：输入变换前图像
OutputArray dst：输出变换后图像，需要初始化一个空矩阵用来保存结果，不用设定矩阵尺寸
InputArray M：变换矩阵，用另一个函数 getAffineTransform() 计算
Size dsize：设置输出图像大小
int flags=INTER_LINEAR：设置插值方式，默认方式为线性插值

生成仿射变换矩阵函数是 getAffineTransform()：

  
cv::Mat cv::getAffineTransform(const Point2f* src, const Point2f* dst)

参数：

const Point2f* src：原图的 3 个固定顶点
const Point2f* dst：目标图像的 3 个固定顶点
注意，顶点数组长度超过 3 个，则会自动以前 3 个为变换顶点；数组可用 Point2f[] 或 Point2f* 表示

透视变换的函数是：

  
void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

参数与 warpAffine() 一致。

生成透视变换矩阵函数是 getPerspectiveTransform()：

  
cv::Mat cv::getPerspectiveTransform(InputArray src, InputArray dst, int solveMethod = DECOMP_LU)

参数：

透视变换顶点为 4 个

桌上有一张扑克牌，我们希望可以从正视的角度观察它。运行以下示例代码观察程序效果：

二、Eigen

1. 简介

Eigen 是C++语言里的一个开源模版库，支持线性代数运算、矩阵和矢量运算、数值分析及其相关的算法。可以将它类比为 python 中的 numpy 。

注意如果想要发挥出 Eigen 的作用，编译时一定要打开 gcc/g++ 编译优化 -O3 。

Eigen 能算得快和它的设计思路有关，涵盖了算法加速的几个方法。

第一，Eigen 使用 Lazy Evaluation 的方法。这个方法的好处是：

把所有能优化的步骤放在编译时去优化。让计算本身尽可能放在最后做，减少内存访问。例如下面一段代码：

  
Eigen::MatrixXd Jacobian_i = Eigen::MatrixXd::Random(10, 10);
Eigen::MatrixXd Jacobian_j = Eigen::MatrixXd::Random(10, 10);
Eigen::MatrixXd Hessian = Eigen::MatrixXd::Zero(10, 10);
Hessian += Jacobian_i.transpose() * Jacobian_j;

实际运行时，在 operator+=() 才真正去做内存读取和计算，而前面的步骤知识更新 flag 。具体见 Eigen/src/Core/EigenBase.h 。

不生成中间变量，减少内存搬运次数，而 Eigen 为了防止矩阵覆盖自己，对矩阵-矩阵乘法会生成一个中间变量。如果我们知道等式左右两边没有相同的项，则可以通知Eigen去取消中间变量。

第二，改变内存的分配方式。使用Eigen时应该尽可能用静态内存代替动态内存。 Eigen::MatrixXd 是如下的缩写：

  
typedef MatrixXd Matrix<double, Dynamic, Dynamic, ColMajor>

MatrixBase 第二和第三个选项是行列的长度，有一项是 Dynamic 就会用动态内存分配。所以已知矩阵大小时应尽可能声明大小，比如 Matrix<double, 10, 10> 。如果内存在整个程序中大小会变，但知道最大可能的大小，都可以告知 Eigen ， Eigen 同样会选择用静态内存。

  
Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::ColMajor, 10, 10> Jacobian_i;
Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::ColMajor, 10, 10> Jacobian_j;
Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::ColMajor, 10, 10> Hessian = Eigen::Matrix<double, 10, 10>::Zero();
Hessian += Jacobian_i.transpose() * Jacobian_j;

静态内存分配不但让我们节省了 new/delete 的开销，还给 Eigen 内部继续优化提供了可能。 Eigen 内置 Single-Instruction-Multiple-Data （SIMD）指令集，对稠密矩阵有很好的优化，如果能触发 CPU SIMD 的指令，能收获成倍的计算效率。

第三，矩阵自身的性质。如果矩阵本身有自身的性质，都可以通知 Eigen ，让 Eigen 用对应的加速方式。比如正定矩阵可以只用上三角进行计算，并且在求解时使用 Eigen::LLT 这样又快又数值稳定的解法等。

2. 安装 Eigen

终端 apt 命令安装：

sudo apt-get install libeigen3-dev

Eigen 只包含头文件，因此它不需要实现编译（只需要使用 #include ），指定好 Eigen 的头文件路径，编译项目即可。Eigen 头文件的默认安装位置是 /usr/include/eigen3 。

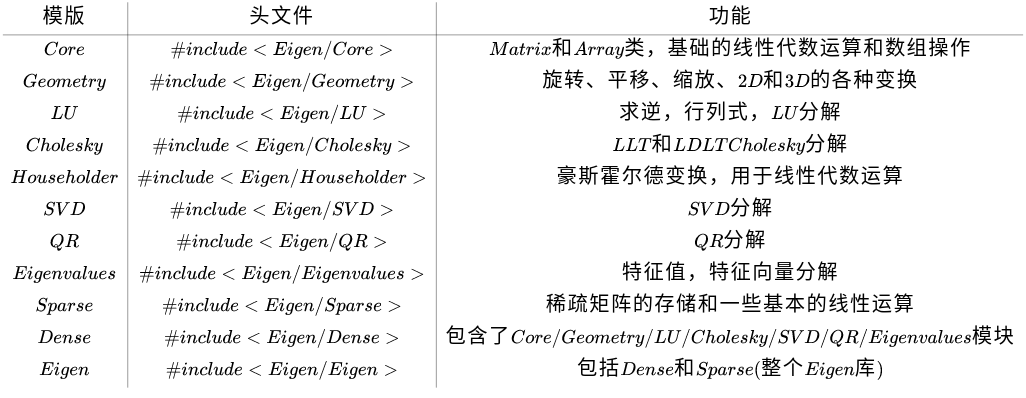
3. Eigen 库的模块及其头文件

为了应对不同的需求， Eigen 库被分为多个功能模块，每个模块都有自己相对应的头文件，以供调用。其中， Dense 模块整合了绝大部分的模块，而 Eigen 模块更是整合了所有模块。

4. 使用方法

（1）构造

  
Eigen::Matrix<double, 3, 3> A;               // Fixed rows and cols. Same as Matrix3d.
Eigen::Matrix<double, 3, Eigen::Dynamic> B;         // Fixed rows, dynamic cols.
Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic> C;   // Full dynamic. Same as MatrixXd.
Eigen::Matrix<double, 3, 3, Eigen::RowMajor> E;     // Row major; default is column-major.

有一些宏定义可以简短代码：

  
typedef Eigen::Matrix<int, 3, 3> Eigen::Matrix2i
typedef Eigen::Matrix<int, Eigen::Dynamic, 3> Eigen::MatrixX3i
typedef Eigen::Matrix<int, 3, Eigen::Dynamic> Eigen::Matrix3Xi

（2）特殊矩阵生成

实例	代码
零矩阵	`Eigen::Matrix<int, 3, 3>::Zero()`
一矩阵	`Eigen::Matrix<int, 3, 3>::Ones()`
单位矩阵	`Eigen::Matrix<int, 3, 3>::Identity()`
常量矩阵	`Eigen::Matrix<int, 3, 3>::Constant(a)`
随机矩阵	`Eigen::Matrix<int, 3, 3>::Random()`
线性空间向量	`Eigen::Vector3i::LinSpaced(a, b)`

（3）随机访问

Eigen 有重载 () 运算符提供随机访问的功能。下面是一段例程：

  
Eigen::MatrixXd m(2,2);
m(0,0) = 3;
m(1,0) = 2.5;
m(0,1) = -1;
m(1,1) = m(1, 0) + m(0, 1);
std::cout << "Here is the matrix m:\n" << m << std::endl;

Eigen::VectorXd v(2);
v(0) = 4;
v(1) = v(0) - 1;
std::cout << "Here is the vector v:\n" << v << std::endl;

（4）赋值

利用重载 << 运算符或 = 运算符完成赋值。下面是一段例程：

  
Eigen::Matrix3f m;
m << 1, 2, 3,
     4, 5, 6,
     7, 8, 9;
std::cout << m << std::endl;

（5）改变矩阵大小

只能作用于大小没有通过模版确定的矩阵，即设置为 Eigen::Dynamic 的维度。

resize(rows, cols) ：可能改变矩阵数据的存储顺序。
conservativeResize(rows, cols)：不会改变矩阵数据的内存分布，因此如果新生成的大小不能覆盖原来的数据，会造成数据丢失。可以减少赋值操作。

下面是一段例程：

  
Eigen::Matrix<int, Eigen::Dynamic, Eigen::Dynamic> m = Eigen::Matrix<int, 3, 3>::Identity();
m.resize(1, 9);

（6）特殊

函数	作用	返回
`transpose`	转置	`Matrix`
`eval`	返回矩阵的数值	`Matrix`
`transposeInPlace`	自身进行转置	`void`
`inverse`	取逆	`Matrix`

需要注意的是，由于 Eigen 使用 Lazy Evaluation，因此 mat = mat.transpose() 是不合法的。

（7）单矩阵运算

函数	作用
`mat.sum()`	返回元素的和
`mat.prod()`	返回元素的乘积和
`mat.maxCoeff()`	返回最大元素
`mat.minCoeff()`	返回最小元素
`mat.trace()`	返回矩阵的迹

（8）子阵运算

block 运算的功能是截取矩阵中的部分元素。

mat.block(i,j,p,q)：动态大小的 block 运算
mat.block<p,q>(i,j)：确定大小的 block 运算

  
Eigen::Matrix<int, 3, 3, 0> matrix_1;
matrix_1.block<2, 2>(0, 0) << Eigen::Matrix2i::Ones();
matrix_1.block<2, 1>(0, 2) << Eigen::Vector2i::Random();
matrix_1.block<1, 3>(2, 0) << 2, 3, 4;
std::cout << matrix_1 << std::endl;

函数	作用
`mat.topLeftCorner(rows, cols)`	取左上角的 block
`mat.topRightCorner(rows, cols)`	取右上角的 block
`mat.bottomLeftCorner(rows, cols)`	取左下角的 block
`mat.bottemRightCorner(rows, cols)`	取右下角的 block
`mat.topRows(rows)`	取上方 k 行
`mat.bottomRows(rows)`	取下方 k 行
`mat.leftCols(cols)`	取左侧 k 行
`mat.rightCols(cols)`	取右方 k 行
`mat.cols(j)`	取第 j 行
`mat.rows(i)`	取第 i 行

（9）广播

将一个矩阵的一个大小为 $1$ 或缺失的维度重复补全后和另一个矩阵进行计算。例如，一个矩阵 A 维度为 $(3, 3)$ ，另一个矩阵B维度为 $(3, 1)$ 。那么运算 $A + B$ 中就发生了广播，矩阵 A 的维度被补全为 $(3, 3)$ 后和 B 进行运算。下面是一段例程：

  
Eigen::MatrixXf mat(2,4);
Eigen::VectorXf v(2);
mat << 1, 2, 6, 9,
       3, 1, 7, 2;
v << 0, 1;
mat.colwise() += v;
std::cout << mat << std::endl;

三、PnP

PnP 常用于单目测距和姿态解算。

如果场景的三维结构已知，利用多个控制点在三维场景中的坐标及其在图像中的透视投影坐标即可求解出摄像机坐标系与表示三维场景结构的世界坐标系之间的绝对位姿关系，包括绝对平移向量 $t$ 以及旋转矩阵 $R$ ，该类求解方法统称为 N 点透视位姿求解（ Perspective-N-Point ， PNP 问题）。这里的控制点是指准确知道三维空间坐标位置，同时也知道对应图像平面坐标的点。对于透视投影来说，要使得 PNP 问题有确定解，需要至少三组控制点。

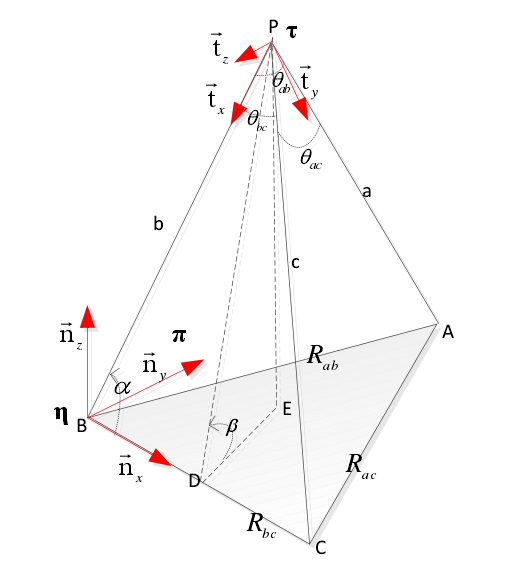
在解决任何 PnP 问题之前，我们都需要准确地标定出相机的内参矩阵和畸变矩阵，标定的质量会影响最后外参矩阵（旋转矩阵+平移矩阵）的精度。这一部分在之前的教程中已经教过了。

1. P3P 问题

P3P 需要利用给定的 3 个点的几何关系。输入数据为 3 对 3D-2D 匹配点。记 3D 点为 A 、 B 、 C ， 2D 点为 a 、 b 、 c 。其中，小写字母代表点的为对应大写字母代表的点在相机成像平面上的投影。此外， P3P 还需要使用一对验证点，从可能的解中选出正确的那一个（验证点记为 D-d ），相机的光心为 O 。请注意，我们知道的是 ABC 三个点在世界坐标系中的坐标，而不是在相机坐标系中的坐标。

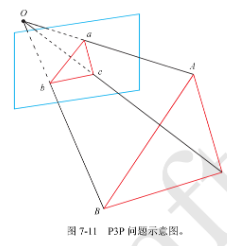
由图可得，显然有如下相似三角形的关系： ${\begin{cases} △ O a b \sim △ O A B \\ △ O b c \sim △ O B C \\ △ O a c \sim △ O A C \end{cases}$ 采用余弦定理，有 ${\begin{cases} O A^{2} + O B^{2} - 2 \cdot O A \cdot O B \cos < a, b >= A B^{2} \\ O B^{2} + O C^{2} - 2 \cdot O B \cdot O C \cos < b, c >= B C^{2} \\ O A^{2} + O C^{2} - 2 \cdot O A \cdot O C \cos < a, c >= A C^{2} \end{cases}$ 左右两边同时除以 $O C^{2}$ ，令 $x = \frac{O A}{O C}, y = \frac{O B}{O C}$ ，有 ${\begin{cases} x^{2} + y^{2} - 2 x y \cos < a, b >= \frac{A B^{2}}{O C^{2}} \\ y^{2} + 1^{2} + 2 y \cos < b, c >= \frac{B C^{2}}{O C^{2}} \\ x^{2} + 1^{2} + 2 x \cos < a, c >= \frac{A C^{2}}{O C^{2}} \end{cases}$ 再令 $u = \frac{A B^{2}}{O C^{2}}, v = \frac{B C^{2}}{A B^{2}}, w = \frac{A C^{2}}{A B^{2}}$ ，有 ${\begin{cases} x^{2} + y^{2} - 2 x y \cos < a, b > - v = 0 \\ y^{2} + 1^{2} + 2 y \cos < b, c > - u v = 0 \\ x^{2} + 1^{2} + 2 x \cos < a, c > - w v = 0 \end{cases}$ 将第一个等式带入后面两个，得： ${\begin{cases} (1 - u) y^{2} - u x^{2} - y \cos < b, c > + 2 u x y \cos < a, b > + 1 = 0 \\ (1 - w) x^{2} - w y^{2} - x \cos < a, c > + 2 w x y \cos < a, b > + 1 = 0 \end{cases}$ 2D 点的图像坐标已知， 3 个余弦角已知。 3D 点的坐标已知，只有 xy 未知。可以采用吴消元法来解上述方程。该方法最多可以获得 4 个解，但可以通过第四个点，来获得最可能的解。进一步地， EPnP （需要 4 对不共面的点）、 UPnP 等则是利用更多的信息来迭代，对相机的位姿进行优化，以尽可能消除噪声的影响。

至于进一步的运算这里就不推倒了，难度有点大，感兴趣的可以看这篇博客。

2. PnP 问题

PnP 和 P3P 问题类似，但是它有足够的信息确定一组解。 PnP 算法通过至少四个点的约束，求出世界坐标系到相机坐标系的旋转矩阵和平移向量。 $[\begin{matrix} u \\ v \\ 1 \end{matrix}] = K [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{matrix}] [\begin{matrix} R & T \\ 0^{T} & 1 \end{matrix}] [\begin{matrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{matrix}]$

3. OpenCV 中的 `solvePnp()`

声明如下：

  
void solvePnP(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int flags=CV_ITERATIVE)

参数：

objectPoints ：视觉坐标系中的点
imagePoints ：像素坐标系中的点
cameraMatrix ：相机内参
disCoeffs ：相机畸变矩阵
rvec ：求出来的旋转向量
tvec ：求出来的平移向量
useExtrinsicGuess：是否输出平移矩阵和旋转矩阵，默认为 false
flags ：选择算法
- SOLVEPNP _ITERATIVE
- SOLVEPNP _P3P
- SOLVEPNP _EPNP
- SOLVEPNP _DLS
- SOLVEPNP _UPNP

如何用这函数来实现测距呢？我们只需要把世界坐标系的原点设置在我们感兴趣的点就可以了，那么函数返回的平移向量的的模长就是相机和那个点的距离。例如

TODO

4. 旋转角度、旋转向量与旋转矩阵

我们再补充一下旋转矩阵和旋转响向量之间的转换关系。

三维空间中的旋转矩阵有 $9$ 个量，而三维空间中的旋转只有 $3$ 个自由度，因此我们很自然地想到，是否可以用更少的量描述一个三维运动。

事实上，对于坐标系的旋转，任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是，我们可以使用一个方向与旋转轴垂直、长度等于旋转角的向量描述旋转运动，这个向量成为旋转向量。

通过这样的方式，我们就可以只通过一个三维的旋转向量和一个三维的平移向量描述三维空间中刚体的运动。

旋转矩阵和旋转向量是可以互相转化的，有旋转向量推导旋转矩阵的公式也被成为罗德里格斯公式： $θ \leftarrow \norm \vec{r} \vec{r} \leftarrow \vec{r} / θ R (\vec{n}, θ) = \cos (θ) I + (1 - \cos θ) \vec{r} {\vec{r}}^{T} + \sin (θ) [\begin{matrix} 0 & - r_{z} & r_{y} \\ r_{z} & 0 & - r_{x} \\ - r_{y} & r_{x} & 0 \end{matrix}]$ 其中，旋转向量的长度（模）表示绕轴逆时针旋转的角度（弧度）， $θ$ 表示旋转角度， $I$ 表示单位矩阵，最后一个矩阵表示 $\vec{r}$ 的反对称矩阵。

旋转角 $θ$ 也可以由公式 $θ = \arccos (\frac{t r (R) - 1}{2})$ 计算得到。

OpenCV 中的旋转向量和旋转矩阵转换的函数是

  
int cvRodrigues2( const CvMat* src, CvMat* dst, CvMat* jacobian=0 );

参数：

src：为输入的旋转向量（ $3 \times 1$ 或者 $1 \times 3$ ）或者旋转矩阵（ $3 \times 3$ ）。该参数向量表示其旋转的角度，用向量长度表示。
dst：为输出的旋转矩阵（ $3 \times 3$ ）或者旋转向量（ $3 \times 1$ 或者 $1 \times 3$ ）。
jacobian：为可选的输出雅可比矩阵（ $3 \times 9$ 或者 $9 \times 3$ ），是输入与输出数组的偏导数。

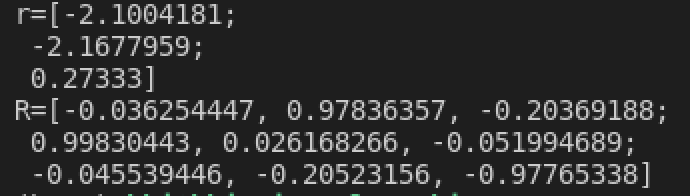
例子如下：

  
cv::Mat r = (cv::Mat_<float>(3,1) << -2.100418, -2.167796, 0.273330);
cv::Mat R(cv::Size(3,3), CV_16FC1);
cv::Rodrigues(r, R);
std::cout << "r=" << r << std::endl;
std::cout << "R=" << R << std::endl;

程序结果：

5. 欧拉角和四元数

（1）欧拉角

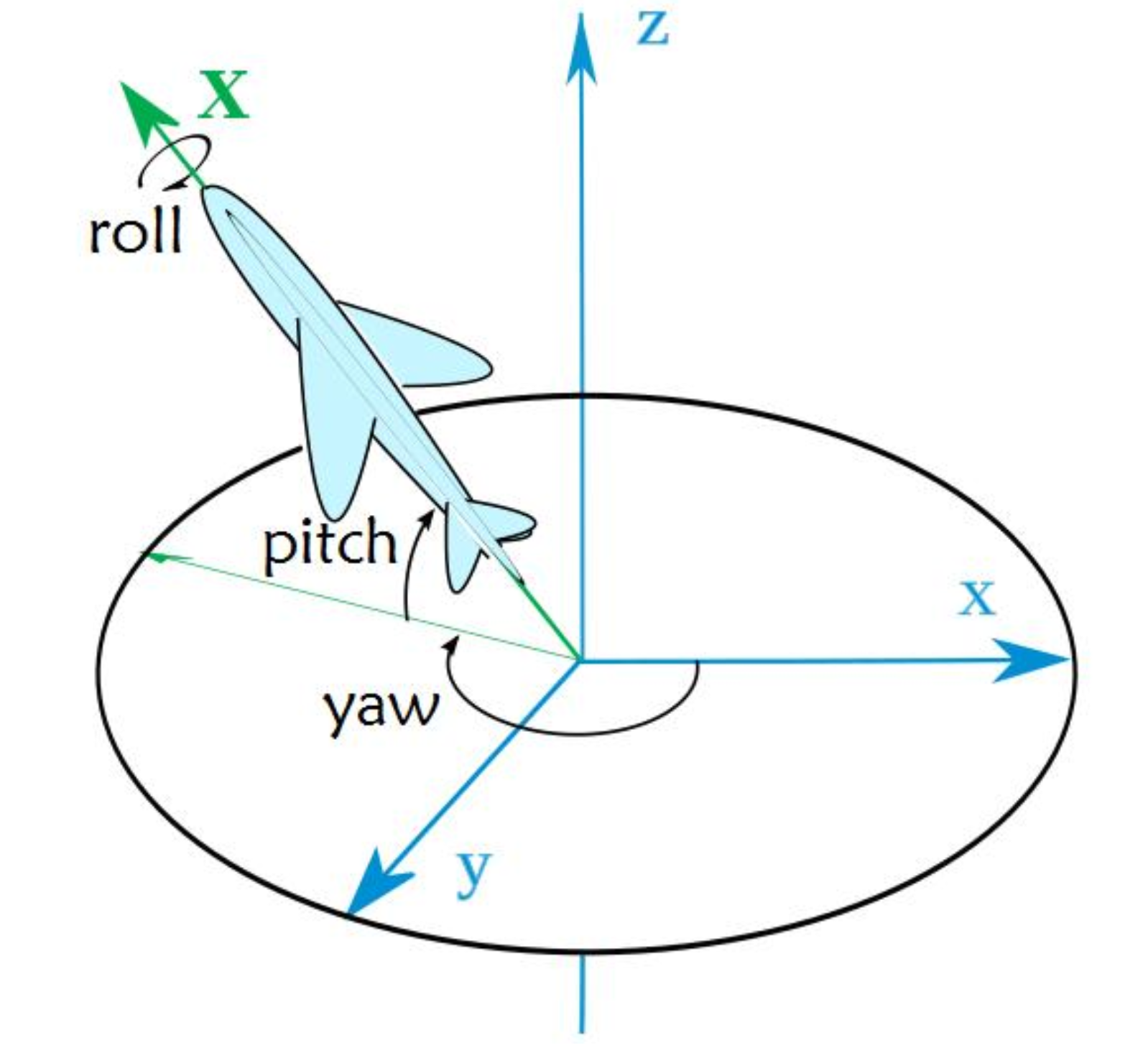
上图是一个示意图。欧拉角定义如下：

绕物体的 z 轴旋转，得到偏航角 yaw
绕旋转之后的 y 轴旋转，得到俯仰角 pitch
绕旋转之后的 x 轴旋转，得到滚转角 roll

如果选用的轴的旋转顺序不同，则欧拉角不同。上述的欧拉角为 $r p y$ 欧拉角，以 $z$ 轴， $y$ 轴， $x$ 轴顺序旋转，是比较常用的一种。

下面举个例子（来自参考资料 5 ）。这里，我把三个 Gimbal 环用不同的颜色做了标记，底部三个轴向， RGB 分别对应 XYZ 。假设现在这个陀螺仪被放在一艘船上，船头的方向沿着 +Z 轴，也就是蓝色右前方。

现在假设，船体发生了摇晃，是沿着前方进行旋转的摇晃，也就是桶滚。由于转子和旋转轴具有较大的惯性，只要没有直接施加扭矩，就会保持原有的姿态。由于上图中绿色的活动的连接头处是可以灵活转动的，此时将发生相对旋转，从而出现以下的情形：

再次假设，船体发生了pitch摇晃，也就是俯仰。同样，由于存在相应方向的可以相对旋转的连接头（红色连接头），转子和旋转轴将仍然保持平衡，如下图：

最后假设，船体发生了yaw摇晃，也就是偏航，此时船体在发生水平旋转。相对旋转发生在蓝色连接头。如下图：

最终，在船体发生 Pitch 、 Yaw 、 Roll 的情况下，陀螺仪都可以通过自身的调节，而让转子和旋转轴保持平衡。

但是欧拉角有一个致命的问题导致死锁，称为万向节死锁。

（2）万向节死锁

现在看起来，这个陀螺仪一切正常，在船体发生任意方向摇晃都可以通过自身调节来应对。然而，真的是这样吗？假如，船体发生了剧烈的变化，此时船首仰起了90度（虽然可能不合理），此时的陀螺仪调节状态如下图：

此时，船体再次发生转动，沿着当前世界坐标的 +Z 轴（蓝色轴，应该正指向船底）进行转动，那么来看看发生了什么情况。

现在，转子不平衡了，陀螺仪的三板斧不起作用了。它失去了自身的调节能力。那么这是为什么呢？

之前陀螺仪之所以能通过自身调节，保持平衡，是因为存在可以相对旋转的连接头。在这种情况下，已经不存在可以相对旋转的连接头了。那么连接头呢？去了哪里？显然，它还是在那里，只不过是，连接头可以旋转的相对方向不是现在需要的按着+Z轴方向。从上图中，我们清楚地看到：

红色连接头：可以给予一个相对俯仰的自由度。
绿色连接头：可以给予一个相对偏航的自由度。
蓝色连接头：可以给予一个相对偏航的自由度。

没错，三个连接头，提供的自由度只对应了俯仰和偏航两个自由度，桶滚自由度丢失了。这就是陀螺仪上的“万向节死锁”问题。

我们可以用小程序来重现万向节死锁问题。首先，预设一下接下来的欧拉角变化顺序。见下图：

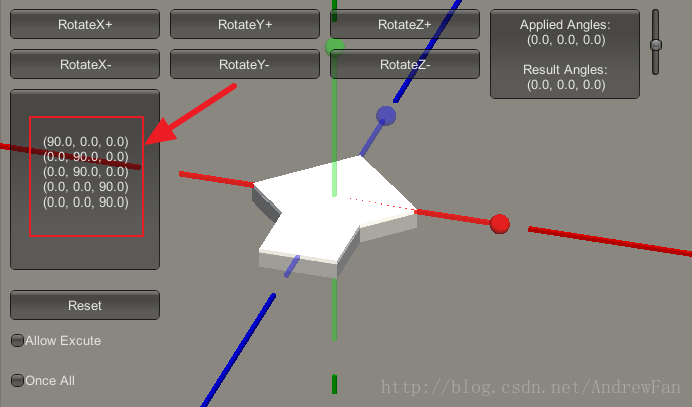
上图中，红色框内的部分的列表，记录了接下来欧拉角的增长变化过程。即它会从 $(0, 0, 0)$ 变化到 $(90, 0, 0)$ ，再变化到 $(90, 90, 0)$ ，再变化到 $(90, 180, 0)$ ，再变化到 $(90, 180, 90)$ ，再变化到 $(90, 180, 180)$ 。下图是变化的过程演示：

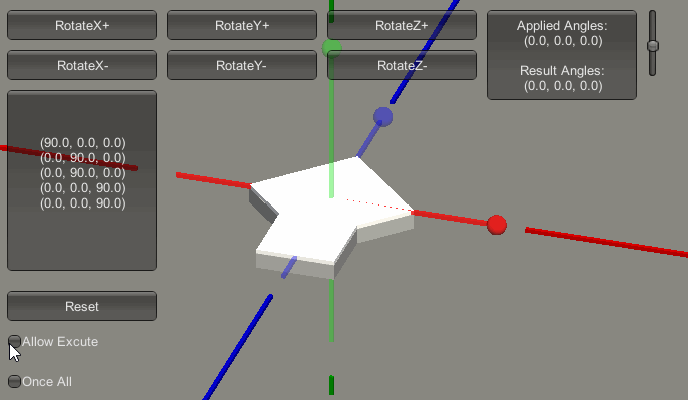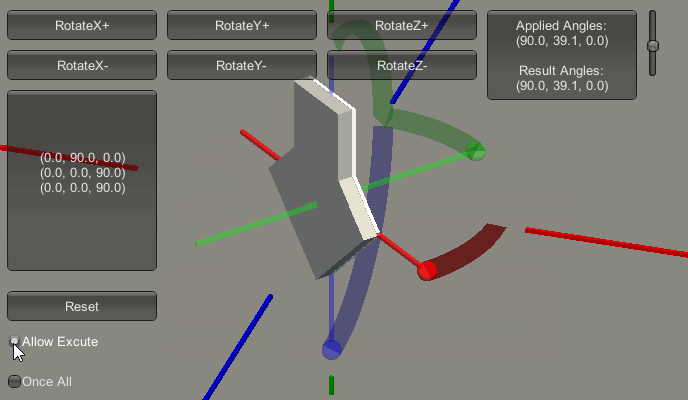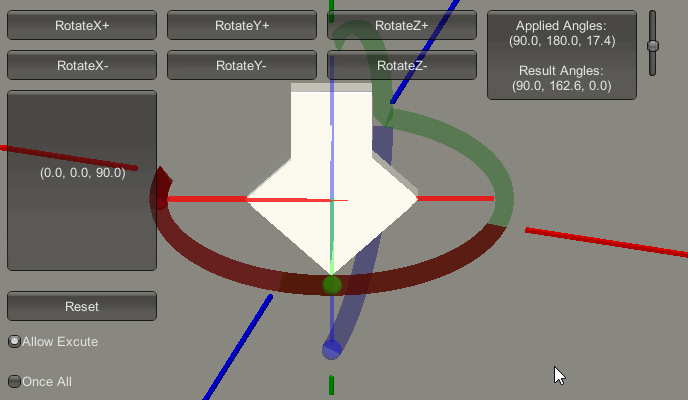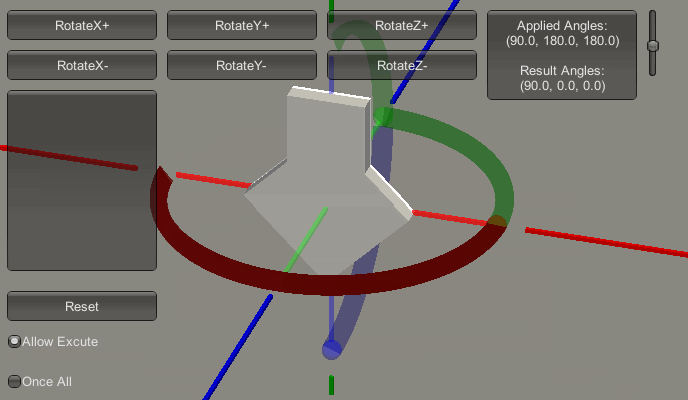
现在可以看到：

当先执行X轴旋转 90 度，此时在执行Pitch(俯仰)变化。
再在Y轴进行变化 0-180 度，此时在执行相对自身的 Roll (桶滚)变化。
再在Z轴进行变化 0-180 度，此时仍在执行相对自身的 Roll (桶滚)变化。

这里所说的俯仰、桶滚、偏航都是相对自己局部坐标系的。这与上述的陀螺仪中出现的问题是一样的，万向节死锁。也就是尽管欧拉角在 XYZ 三个轴向进行进动(持续增长或者减少)，但是影响最终的结果，只对应了两个轴向。这一点在 Unity 编程中也应该注意。

为了解决这一问题，我们引入四元数。由于万向锁的存在，欧拉角并不是一个完备的描述旋转的方式。事实上，我们找不到不带奇异性的三维向量描述方式。

（3）四元数

四元数的定义如下： $q = {[\begin{matrix} w & x & y & z \end{matrix}]}^{T}, where | q |^{2} = 1$ 定义 $ψ, θ, ϕ$ 分别为绕Z轴、Y轴、X轴的旋转角度，如果用 Tait-Bryan angle 表示，分别为 Yaw 、 Pitch 、 Roll 。

旋转角度->四元数

通过旋转轴和绕该轴旋转的角度可以构造一个四元数： $w = \cos (α / 2) x = \sin (α / 2) \cos (β_{x}) y = \sin (α / 2) \cos (β_{y}) z = \sin (α / 2) \cos (β_{z})$ 其中 $α$ 是绕旋转轴旋转的角度， $\cos (β_{x}), \cos (β_{y}), \cos (β_{z})$ 为旋转轴在 $x, y, z$ 方向的分量（由此确定了旋转轴)。

欧拉角->四元数

q = [\begin{matrix} w \\ x \\ y \\ z \end{matrix}] = [\begin{matrix} \cos (ϕ / 2) \cos (θ / 2) \cos (ψ / 2) + \sin (ϕ / 2) \sin (θ / 2) \sin (ψ / 2) \\ \sin (ϕ / 2) \cos (θ / 2) \cos (ψ / 2) - \cos (ϕ / 2) \sin (θ / 2) \sin (ψ / 2) \\ \cos (ϕ / 2) \sin (θ / 2) \cos (ψ / 2) + \sin (ϕ / 2) \cos (θ / 2) \sin (ψ / 2) \\ \cos (ϕ / 2) \cos (θ / 2) \sin (ψ / 2) - \sin (ϕ / 2) \sin (θ / 2) \cos (ψ / 2) \end{matrix}]

四元数->欧拉角

[\begin{matrix} ϕ \\ θ \\ ψ \end{matrix}] = [\begin{matrix} atan2 (2 (w x + y z), 1 - 2 (x^{2} + y^{2})) \\ \arcsin (2 (w y - z x)) \\ atan2 (2 (w z + x y), 1 - 2 (y^{2} + z^{2})) \end{matrix}]

其他坐标系

在其他坐标系下，需根据坐标轴的定义，调整一下以上公式。如在 Direct3D 中，笛卡尔坐标系的 X 轴变为 Z 轴， Y 轴变为 X 轴， Z 轴变为 Y 轴（无需考虑方向）。 $q = [\begin{matrix} w \\ x \\ y \\ z \end{matrix}] = [\begin{matrix} \cos (ϕ / 2) \cos (θ / 2) \cos (ψ / 2) + \sin (ϕ / 2) \sin (θ / 2) \sin (ψ / 2) \\ \cos (ϕ / 2) \sin (θ / 2) \cos (ψ / 2) + \sin (ϕ / 2) \cos (θ / 2) \sin (ψ / 2) \\ \cos (ϕ / 2) \cos (θ / 2) \sin (ψ / 2) - \sin (ϕ / 2) \sin (θ / 2) \cos (ψ / 2) \\ \sin (ϕ / 2) \cos (θ / 2) \cos (ψ / 2) - \cos (ϕ / 2) \sin (θ / 2) \sin (ψ / 2) \end{matrix}]$

[\begin{matrix} ϕ \\ θ \\ ψ \end{matrix}] = [\begin{matrix} atan2 (2 (w z + x y), 1 - 2 (x^{2} + z^{2})) \\ \arcsin (2 (w x - y z)) \\ atan2 (2 (w y + x z), 1 - 2 (x^{2} + y^{2})) \end{matrix}]

三、作业

链接: https://pan.baidu.com/s/19jWghlU5FS9YfwG4EcMADA 提取码: q5bg

【其中部分题目提供了参考答案】

对数据包中的汽车照片中的车牌进行透视变换，可自行决定难度：
1. 通过画图工具等手动确定透视变换 4 个像素点坐标
2. 通过 OpenCV 窗口鼠标回调函数点击确定像素点坐标
3. 通过传统视觉识别确定像素点坐标
项目实战：对桌面的扑克牌进行透视变换，给出扑克牌的正视图。要求用算法识别出角点并排序。
效果如下：
使用 PnP 算法求解相机相对于标定板的位置，相机标定结果已经在数据包中给出与 hw3.zip 压缩包。
使用 OpenCV （与 Eigen ）完成深度图重投影，文件位于 hw4.zip 压缩包，其中包含了图片、其对应的深度信息、以及相机内参矩阵与相机透视变换矩阵。

如果觉得本教程不错或对您有用，请前往项目地址 https://github.com/Harry-hhj/Harry-hhj.github.io 点击 Star :) ，这将是对我的肯定和鼓励，谢谢！

四、参考资料

作者：Harry-hhj，Github主页：传送门

作者：E-T-E-R-N-A-L-B-L-U-E，传送门

RM 教程 5 —— 单目视觉

RM 教程 5 —— 单目视觉

一、仿射变换与透视变换

0. 再谈其次坐标系

1. 线性变换

1. 仿射变换

补充知识

平移变换 Translation

缩放变换 Scale

剪切变换 Shear

旋转变换 Rotation

组合

2. 透视变换

3. OpenCV中的仿射变换和透视变换

二、Eigen

1. 简介

2. 安装 Eigen

3. Eigen 库的模块及其头文件

4. 使用方法

（1）构造

（2）特殊矩阵生成

（3）随机访问

（4）赋值

（5）改变矩阵大小

（6）特殊

（7）单矩阵运算

（8）子阵运算

（9）广播

三、PnP

1. P3P 问题

2. PnP 问题

3. OpenCV 中的 solvePnp()

4. 旋转角度、旋转向量与旋转矩阵

5. 欧拉角和四元数

（1）欧拉角

（2）万向节死锁

（3）四元数

旋转角度->四元数

欧拉角->四元数

四元数->欧拉角

其他坐标系

三、作业

四、参考资料

Further Reading

RM 教程 6 —— 特征点，双目相机与光流

RM 教程 1 —— Linux 教程

RM 教程 2 —— 安装 OpenCV

Trending Tags

3. OpenCV 中的 `solvePnp()`