Deconvolution

一、概念

逆卷积（Deconvolution）一般和转置卷积（transposed conv）、微步卷积（fractionally strided conv）的叫法等价。其常见的用处包括：

• 在 ZF-Net 中用于对 feature map 做可视化
• 在 FCN 中用于生成等于原图 shape 的图像
• 无监督的 autoencoder 和 deconvNet 中用于解码器
• DSSD、GAN中的应用
• ……

从上面可以看出，deconvolution 最大的用处是：对 feature map 进行升采样，这和双线性插值（bilinear interpolation）类似。

注意，它虽然叫做逆卷积，但是它并不是卷积的逆过程，不能完全还原出卷积前的输入，与原输入仅仅在大小上相同，在数值上虽然具有一定的相关性，但是没有可逆关系。deconv 仅仅是一个普通的卷积层，在神经网络中也是需要通过梯度下降去学习的。在 Pytorch 中通过 torch.nn.ConvTranspose2d 实现，使用方法参考这篇教程。

二、最基本的三种形式

注：以下推导时，假设长和宽大小相等，如果大小不等，只需要按照以下操作分别计算就行了。

1. 无 padding 、无 stride

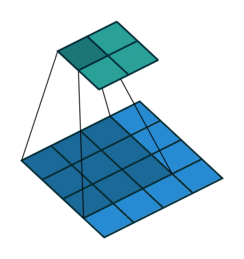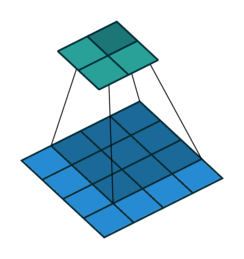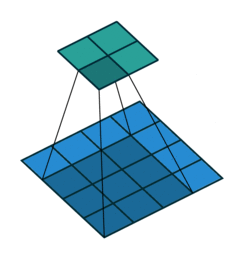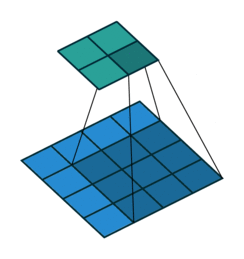
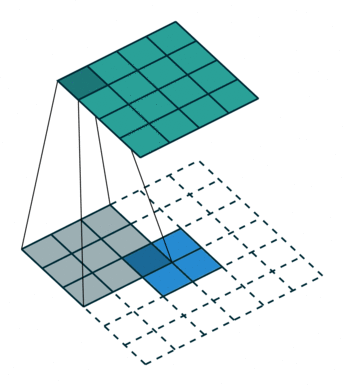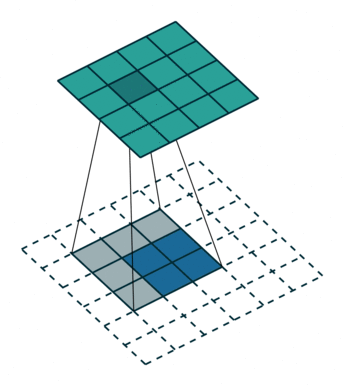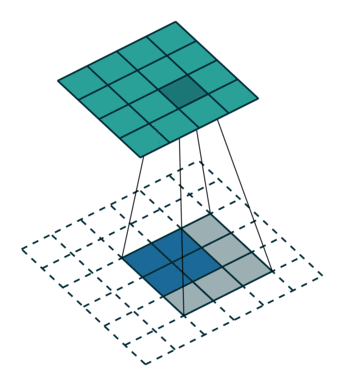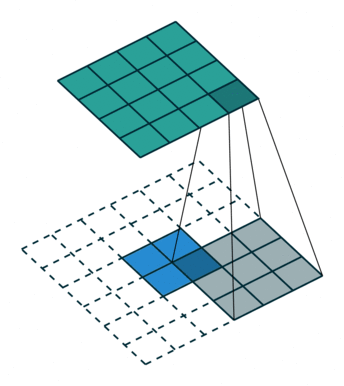
首先我们来看看最基本的卷积形式：对于 $(m \times m)$ 的特征图 $I$ ，用大小为 $(k \times k)$ 的核做卷积，则得到的特征图 $O$ 大小为 $((m-k+1) \times (m-k+1))$ 。怎么让特征图 $O$ 经过同样大小的卷积核以后的到和特征图 $I$ 一样的大小呢？我们先对特征图 $O$ 做 $padding=k-1$ 的填充，大小变为 $((m+k-1) \times (m+k-1))$ ，再用等大的 $(k \times k)$ 核做卷积，则得到的特征图 $I’$ 的大小是 $(m \times m)$ 。

2. 无 padding 、有 stride

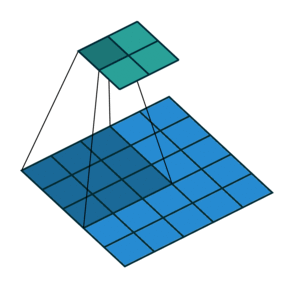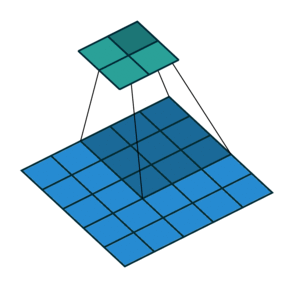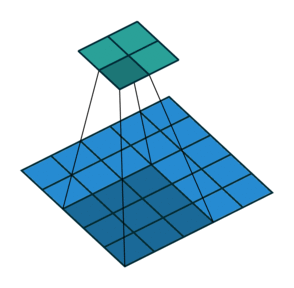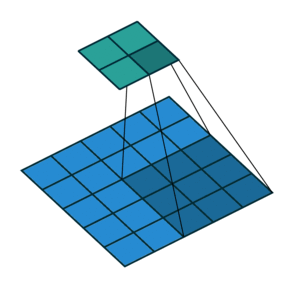
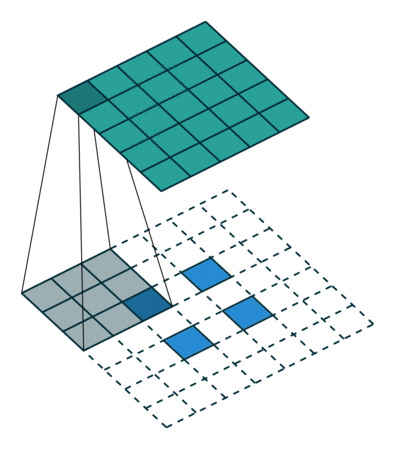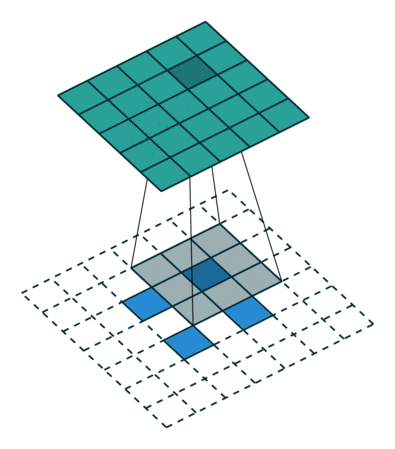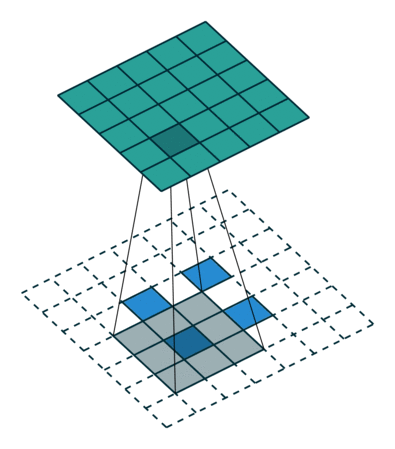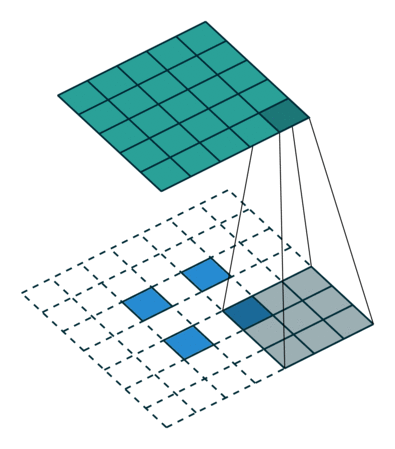
然后我们来看看加入 stride 后如何 deconv ：对于 $(m \times m)$ 的特征图 $I$ ，用 $(k \times k)$ 大小的核做卷积，记 stride 为 $s$ ，则得到的特征图 $O$ 的大小为 $((\lfloor \cfrac{m-k}{s}+1 \rfloor) \times (\lfloor \cfrac{m-k}{s}+1 \rfloor))$ 。怎么让特征图 $O$ 经过同样大小的卷积核以后的到和特征图 $I$ 一样的大小呢？与之前不同的是，我们需要根据 stride 对 $I$ 做内部扩充（填 $0$），具体的规则是：在两个元素之间加入 $s-1$ 个 $0$ ，共有 $\lfloor \cfrac{m-k}{s}+1 \rfloor - 1$ 个插入点。再和之前一样，加入 $padding=k-1$ 的填充，得到 $O’$ 。此时计算可得 $O’$ 的边长为为 $\lfloor \cfrac{m-k}{s}+1 \rfloor + 2(k-1) + (s-1)(\lfloor \cfrac{m-k}{s}+1 \rfloor-1) = m+k-1$ ，即大小为 $(m-k+1, m-k+1)$ ，用等大的 $(k \times k)$ 核做卷积之后得到的特征图 $I’$ 的大小是 $(m \times m)$ 。

另 s=1 就得到 [1] 中的情况。

3. 有 padding 、无 stride

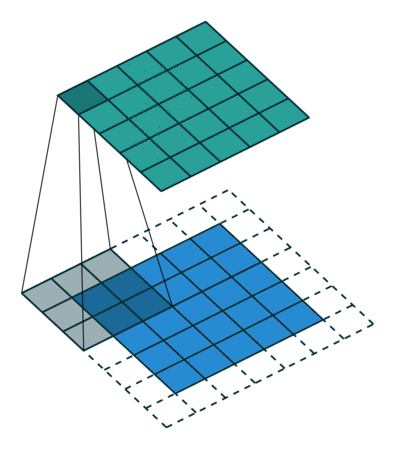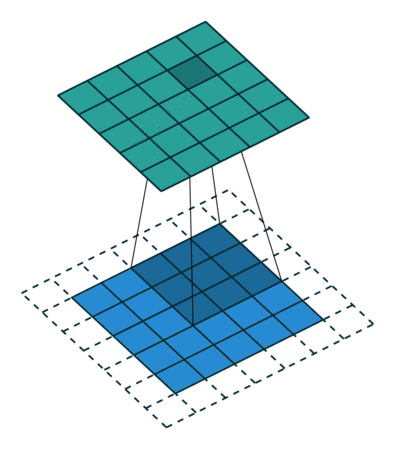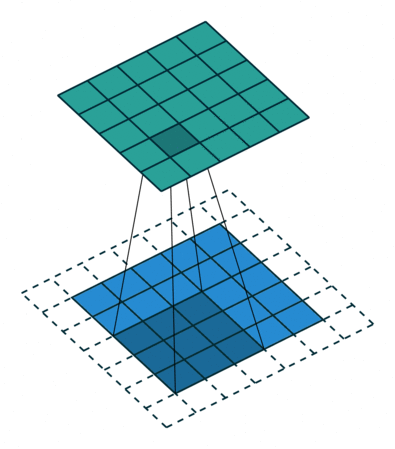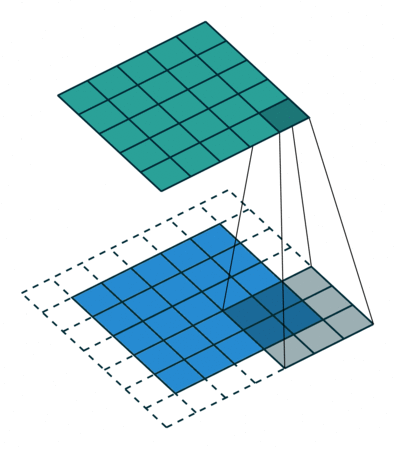
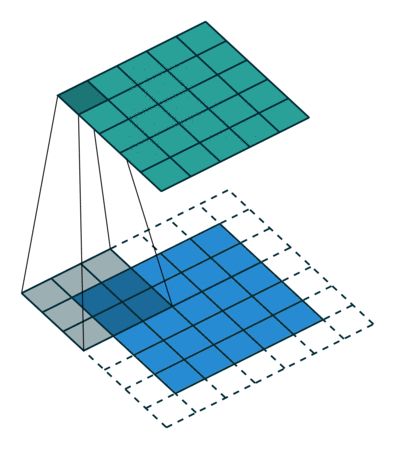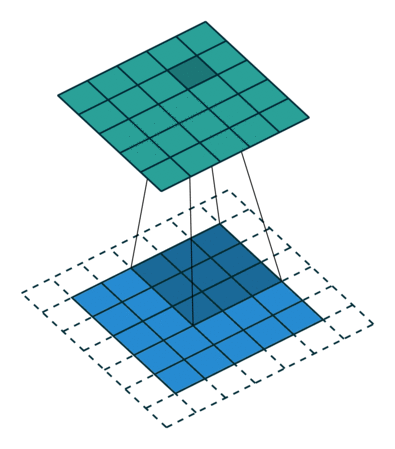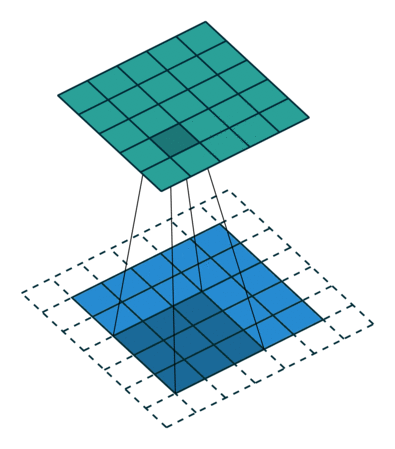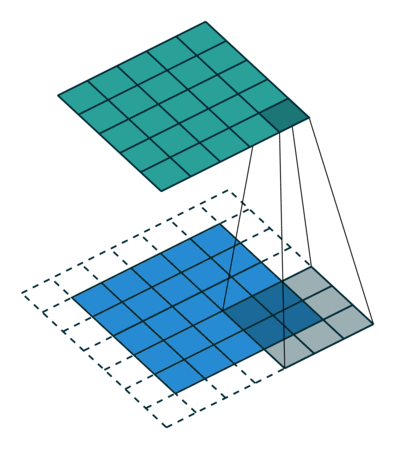
为了方便了解加入 padding 之后我们应该如何操作，我们先不考虑 stride 带来的影响，即令 stride=1 。对于大小为 $(m \times m)$ 的特征图 $I$ ，先做大小为 $p$ 的 padding ，用 $(k \times k)$ 的核做卷积，则得到的特征图 $O$ 的大小为 $((m+2p-k+1) \times (m+2p-k+1))$ 。怎么让特征图 $O$ 经过同样大小的卷积核以后的到和特征图 $I$ 一样的大小呢？我们先假设我们对 $O$ 做大小为 $p’$ 的 padding 得到 $O’$ ，再用等大的 $(k \times k)$ 的核做 stride=1 的卷积，则得到的特征图 $I’$ 的边长是 $(m+2p-k+1)+2p’-k+1$ ，最终需要得到大小为 $(m \times m)$ 的特征图 $I’$ 。那么得到以下等式： \((m+2p-k+1)+2p'-k+1 = m\) 得到 \(p' = k-1-p\) 。

三、公式推导

接下来我们考虑最一般的情况（不考虑长宽不等，因为计算过程相同）。

对于大小为 $(m \times m)$ 的特征图 $I$ ，先做大小为 $p$ 的 padding ，得到 $I’$ 的大小为 $((m+2p) \times (m+2p))$ ，卷积后得到特征图 $O$ 的大小为 $((\cfrac{m+2p-k}{s}+1) \times (\cfrac{m+2p-k}{s}+1))$ 。

对 $O’$ 进行 deconv ，先做大小为 $p’$ 的 padding 得到 $O’$ ，边长为 $\lfloor \cfrac{m+2p-k}{s}+1 \rfloor + 2p’$ 。然后根据 stride 填充得到 $O’’$ ，边长为 $\lfloor \cfrac{m+2p-k}{s}+1 \rfloor + 2p’+(s-1)(\lfloor \cfrac{m+2p-k}{s}+1 \rfloor - 1)$ 。再用等大的 $(k \times k)$ 的核做 stride=1 的卷积，则得到的特征图 $I’’$ 的边长是 $\lfloor \cfrac{m+2p-k}{s}+1 \rfloor + 2p’+(s-1)(\lfloor \cfrac{m+2p-k}{s}+1 \rfloor - 1) -k+1$ ，令 $I’’$ 的边长为 $m$ （我们的目标），可得等式： \(\lfloor \cfrac{m+2p-k}{s}+1 \rfloor + 2p'+(s-1)(\lfloor \cfrac{m+2p-k}{s}+1 \rfloor - 1) -k+1 = m\) 解得 \(p'=k-1-p\) 。

四、总结

我们来做一个总结，假设特征图 $I$ 大小为 $(m \times m)$ ，经过大小为 $(k \times k)$ 卷积核 kernel ，padding 的大小为 $p$ ， stride 的大小为 $s$ 的卷积，得到特征图 $O$ 。 deconv 的操作可以归为两步，分别是：

1. 将卷积核 kernel 做行列转置，得到 kernel'
2. 对特征图 $O$ 根据 stride 做内部填充，填充规则是：在每两行/列元素之间插入 $s-1$ 行/列的 $0$ ，得到特征图 $O’$
3. 对特征图 $O’$ 做 padding ，大小为 $k-1-p$ ，得到特征图 $I’$ ，此时 $I’$ 的大小和 $I$ 相同，但数据不同

我们可以发现：stride 仅和填充的大小有关，而 deconv 的实际卷积操作是 stride=1 的。

五、解释

为什么逆卷积可以一定程度上还原卷积操作呢？这里简单说明一下逆卷积和卷积的关系：

1. 特征图大小相似
2. 保证了同样的连通性

什么是同样的连接性？这是指从 $I$ 到 $O$ （ $I$ 、 $O$ 分别表示卷积前和卷积后的特征图），如果中 $I$ 一个位置与 $O$ 中一个位置通过 kernel 有关系，那么在卷积核逆卷积中有相同的连通。

六、一般情况

如果我们不需要 deconv 的输出与原输入卷积的特征图大小相同，那么这就是最一般的情况。此时我们不再限制 stride 和 padding 的大小，而是根据它们计算 deconv 输出的大小，其实这在 [三] 中已经推导过了：

输入大小：$(N, C_{in}, H_{in}, W_{in})$

输出大小：$(N, C_{out}, H_{out}, W_{out})$

其中： \(H_{out} = (H_{in}-1) \times \text{stride}[0] - 2 \times \text{padding}[0] + \text{dilation}[0] \times (\text{kernel\_size[0]}-1) + \text{out\_padding}[0] + 1 \\ W_{out} = (W_{in}-1) \times \text{stride}[1] - 2 \times \text{padding}[1] + \text{dilation}[1] \times (\text{kernel\_size[1]}-1) + \text{out\_padding}[1] + 1\)

七、out_padding

在上面的式子中，出现了一个新的参数 - out_padding ，但其只用于查找输出形状，但实际上并不向输出添加零填充。

我们先来提出一个问题：假定输入特征图为 $(6 \times 6)$ ， stride=2 ， kernel_size=3 ，进行 same 卷积操作得到输出特征图的大小为 $(3 \times 3)$ 。再假讨论另一种情况，假定输入特征图为 $(5 \times 5)$ ， stride=2 ， kernel_size=3 ，这时候设置 padding=1 ，那么也会得到输出特征图为 $(3 \times 3)$ 。如果继续考虑 valid 卷积，那么会有更多的情况得到相同大小的输出特征图。这在进行逆卷积的时候就出现了问题，因为卷积时是多种情况对应到了一种情况，那么逆卷积时该如何对应回去呢？

解决的方法就是使用 out_padding 参数，它的作用是：当 $\text{stride} \gt 1$ 时， Conv2d 将多个输入形状映射到相同的输出形状。output_padding 通过在一边有效地增加计算出的输出形状来解决这种模糊性。

首先我们要认可一个前提：在大多数情况下我们都希望经过卷积/反卷积处理后的图像尺寸比例能够被步长整除，即 $输入特征图大小/输出特征图大小=stride$ ，也就是 same 模式。所以我们通过添加 out_padding 这一参数来使得结果满足这一前提，那么 deconv 的输出特征图大小就能够满足为 $其输入大小*stride$ ，而不是任意可能的大小。这样的好处是：网络在后面进行预尺寸相关的操作时，输入的大小是已知且固定的。

实现方法：

对于 conv 一般推荐的 padding 是 (kernel_size-1)/2 ，那么对于 deconv 来说为了满足前提有如下的等式（假设 dilation 为 $1$）： \(\begin{equation}\begin{split} H_{out} & = (H_{in}-1) \times \text{stride}[0] - 2 \times \text{padding}[0] + \text{dilation}[0] \times (\text{kernel\_size[0]}-1) + \text{out\_padding}[0] + 1 \\ & = (H_{in}-1) \times \text{stride}[0] - (\text{kernel\_size}[0]-1) + \text{dilation}[0] \times (\text{kernel\_size[0]}-1) + \text{out\_padding}[0] + 1 \\ \end{split}\end{equation}\) 得到 \(\text{out\_padding}[0] = \text{stride}[0]-1\)。out_padding[1] 同理。

当然可以取其他值，不妨碍 deconv 的计算，但是需要注意，网络后面进行尺寸有关的操作时输入的大小可能不能确定。

如果觉得本教程不错或对您有用，请前往项目地址 https://github.com/Harry-hhj/Harry-hhj.github.io 点击 Star :) ，这将是对我的肯定和鼓励，谢谢！

八、参考文献

1. Deconvolution（逆卷积）
2. Convolution arithmetic
3. ConvTranspose2d原理，深度网络如何进行上采样？
4. nn.ConvTranspose2d的参数output_padding的作用

作者：Harry-hhj，github主页：传送门